3. ¡Hacia el infinito y más allá!
 |
| 5. Imagen de Inti bajo licencia Creative Commons. |
Pues bien, vamos a calcular las asíntotas y ver dónde está la función en el infinito.
Comenzamos con la asíntota vertical.
Si recuerdas, en el tema 1 de esta unidad, definimos el dominio de una función como el conjunto de valores que tomaba la variable independiente "x". Esto es lo mismo que decir, que el dominio son todos los números que se le puede dar a x.
En las funciones del tema anterior no había ningún problema. Las funciones eran de la forma y = mx + n, y como siempre se puede multiplicar y sumar, no teníamos ninguna restricción para el dominio de la función. El dominio era todos los números reales:
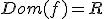
En las funciones cuadráticas tampoco, pues siempre se puede elevar al cuadrado un número y sumarle un producto, por lo que el dominio también es el conjunto de todos los números reales.
Pero, ¿ocurre lo mismo en las funciones que estamos viendo ahora?, o sea, en las funciones
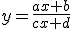
¿Has probado a dividir alguna vez por cero? Cógete una calculadora y divide cualquier cantidad por cero. ¿Qué ocurre? Que tururú, que eso no existe. Claro, ¿cómo vas a repartir 10 caramelos entre cero niños? Si no hay a quien dárselos.
Por tanto, en las funciones racionales, el dominio son todos los números reales, salvo los que hagan cero el denominador de la función.
Pues ahí es donde van a estar los puntos candidatos a que haya asíntota vertical; los puntos donde la función se corta y al no entrar en el dominio no aparecerán pintados.
Cógete otra vez la calculadora, y ahora en lugar de dividir un número por cero, vamos a dividirlo por un número muy pequeño, por ejemplo, 0.1. Y por otro más pequeño, 0.01, ó 0.000001. ¿Qué es lo que ocurre?, cada vez nos sale un número más grande, cada vez nos vamos más al infinito. Luego ahí tenemos la asíntota vertical; cuando dividimos por algo muy próximo a cero.
Entonces, para buscar la asíntota vertical, habrá que buscar el punto donde se anula el denominador, o dicho de otra manera, la asíntota vertical está en el punto que no entra en el dominio de la función.
Una función racional de la forma
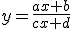 tiene una asíntota vertical. Para buscarla, buscamos el valor de "x" que haga que el denominador sea cero, y ese será el valor de "x" que nos da la asíntota vertical
tiene una asíntota vertical. Para buscarla, buscamos el valor de "x" que haga que el denominador sea cero, y ese será el valor de "x" que nos da la asíntota vertical
- cx + d = 0, y resolvemos.
- x = -d/c es la asíntota vertical.
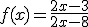 tiene como asíntota vertical la recta x = 4.
tiene como asíntota vertical la recta x = 4.
Verdadero Falso
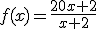
Verdadero Falso
 |
| 6. Imagen de RaidersLight bajo licencia Creative Commons |
Veamos ahora cómo determinar la asíntota horizontal:
La asíntota horizontal, es la recta a la que se va pegando la función cuando "x" toma valores muy grandes, positivos o negativos.
Vamos a cogernos una función concreta, por ejemplo:
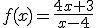
¿A qué se acercará la función si le damos valores muy grandes a x?.
Pues vamos a dárselos. Si x = 100, f(100) = 4.19; si x = 500, f(500) = 4.03; si x = 1000, f(1000) = 4.019.
Parece que mientras mayor sea el valor de x, más se va acercando la función a 4.
Pero, ¿cómo saberlo sin tener que hacer esos cálculos?. Pues muy fácil, fíjate, cuando hemos calculado f(1000), la operación que hemos hecho es:
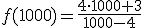
Pero ¿realmente es importante sumar 3 a 4000? Si yo tengo 4000 €, 3 euros más o 3 euros menos no me supone mucho. Lo mismo ocurre en el denominador, el 4 que está restando no hace mucho si se le está quitando a 1000.
Así, si estamos dándole a "x" valores grandes, los coeficientes "b" y "d" que están sumando los podemos suprimir, pues no aportan demasiado.
Luego si x es muy grande,
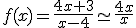
y simplificando, nos quedamos que cuando x es grande, la función es aproximadamente 4.
Para calcular la asíntota horizontal de una funcional racional de este tipo, dividimos los coeficientes que multiplican a las "x" en el numerador y en el denominador.
Si 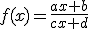 , la asíntota horizontal es y = a/c.
, la asíntota horizontal es y = a/c.
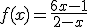 tiene como asíntota horizontal
tiene como asíntota horizontal
|
x=2
| |
|
y=6
| |
|
y=3
| |
|
y= -6
|
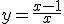 tiene por asíntota horizontal la recta:
tiene por asíntota horizontal la recta:
|
y=1
| |
|
y=0
| |
|
y=2
|
Como dijimos al final del punto anterior, una vez que sabemos cuáles son las asíntotas, representar este tipo de función es muy fácil, pues sabiendo a las rectas que se han de pegar, sólo debemos dar unos cuantos valores a la función para ajustar la gráfica.
En la siguiente escena puedes ver varios ejemplos resueltos.
Applet de IFSTIC bajo licencia Creative Commons.
Realiza la actividad que aparece al pulsar sobre el enlace.
Representa las funciones que aparecen en la siguiente escena.
Mueve el punto verde para colocar la asíntota horizontal, el rojo para la vertical y el azul como un punto de la gráfica que se use como referencia.
Utiliza el zoom si es necesario para visualizar la región buena para representarla.
Applet de Joaquín García Mollá en i-matematicas.com bajo licencia Creative Commons.
Si recuerdas, en el tema anterior vimos un último apartado donde hablábamos de las funciones de oferta y demanda.
En ese tema las tratábamos como funciones lineales o afines, pero no siempre tiene por qué ser así. Estas funciones pueden ser también como las que hemos visto en este tema, o sea, cuadráticas o racionales, o incluso como las que veremos en temas siguientes.
Todo el estudio en cuanto a significado y búsqueda del punto de equilibrio se hace exactamente igual que como lo vimos en el tema anterior.