2.2 Las cosas cada una en su sitio.
 |
| 2. Foto de Vicintosh.com bajo licencia Creative Commons |
Se llaman parámetros de posición aquellos que dividen a los datos obtenidos en partes proporcionales, de forma que cada parte tenga el mismo número de elementos. Para poder hacerlo necesitamos que los datos estén ordenados de menor a mayor.A veces se les llama con el nombre genérico de cuantiles. Los hay de tres tipos: cuartiles, deciles y percentiles, aunque vamos a desarrollar el primero y el último.
Q1: primer cuartil, tiene el 25% de los datos delante de él y el 75% detrás.
Me: segundo cuartil, que coincide con la mediana. Tiene el 50% de los datos delante y el otro 50% detrás de él.
Q3: Deja delante de él el 75% de la distribución y detrás el 25%.
Se define el recorrido intercuartílico a la diferencia entre el tercero y el primer cuartil. Dentro de este intervalo se encuentra el 50% de la distribución. Un estudio conjunto del recorrido y del recorrido intercuartílico nos da información sobre la dispersión de la muestra. Si el recorrido general es grande pero el intercuartílico pequeño, eso indica que hay valores extremos. Si ambos son grandes los datos son dispersos y si ambos son pequeños los datos están muy agrupados respecto a los valores centrales.
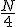 y el primer valor cuya frecuencia absoluta acumulada supera ese valor es Q1. Para Q3 debemos hallar
y el primer valor cuya frecuencia absoluta acumulada supera ese valor es Q1. Para Q3 debemos hallar 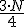 y seleccionar aquel valor cuya frecuencia acumulada supera esa cantidad. Hay que recordar, como en la mediana, que si un valor tiene como frecuencia acumulada exactamente ese valor se halla la media aritmética con el valor siguiente.
y seleccionar aquel valor cuya frecuencia acumulada supera esa cantidad. Hay que recordar, como en la mediana, que si un valor tiene como frecuencia acumulada exactamente ese valor se halla la media aritmética con el valor siguiente.
 |
Para realizar un estudio sobre el gasto farmacéutico en la sanidad pública, le encargan a Mercedes que haga un estudio sobre el número de medicamentos por paciente que se receta en una determinada consulta a lo largo de una semana. Se obtiene la siguiente tabla.
| nº de medicamentos (xi) | 1 | 2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| nº de pacientes (fi) | 12 | 24 |
15 |
13 |
9 |
6 |
2 |
1 |
1 |
1 |
Calcula los cuartiles de esa distribución.
De forma análoga a los cuartiles, para hallarlos hay que dividir el número total de datos (N) entre 100 y multiplicarlo por el orden del percentil que se busca y después hallar que valor iguala o sobrepasa a esa cantidad.
Igual que hay unos parámetros que dividen el conjunto de los valores en 100 partes iguales, existen los deciles que la dividen en 10 partes iguales, pero en lugar de los deciles se suelen utilizar más los percentiles.
Ya para acabar este apartado vamos a ver que ocurre con estos parámetros de posición cuando tenemos la variable agrupada en intervalos. En este caso el cuartil o el percentil que se busca suele estar dentro de un intervalo y para ajustar exactamente el valor debemos hacer una regla de tres. Vamos a ver en el siguiente ejemplo como calcular los percentiles es igual que los cuartiles con la diferencia de dividir N entre 100 en lugar de entre cuatro y multiplicar por el número del percentil correspondiente.
 |
Considera la distribución del ejemplo de las medidas de los espárragos que estamos trabajando en este tema.
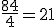 luego Q1 = 2
luego Q1 = 2
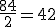 luego Me = 3
luego Me = 3
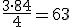 y por tanto Q3 = 4
y por tanto Q3 = 4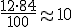 y el P12 = 1
y el P12 = 1
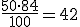 y entonces P50 =3
y entonces P50 =3
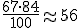 luego el P67 = 4
luego el P67 = 4