3. ¡Por mis bigotes!
 |
| 3. Imagen de ruyman gilbert bajo licencia Creative Commons. |
El nuevo gráfico recibe el vistoso nombre de Diagrama de Caja y Bigotes (box and whiskers en inglés) y para representarlo se utilizan los cuartiles y el valor menor y mayor de la distribución, en definitiva, el recorrido.
Para construirlo se dibuja un rectángulo del grosor que se quiera pero cuyo largo es igual al recorrido intercuartílico. Dentro del rectángulo se dibuja una línea para indicar la mediana. Esa caja se completa con dos líneas que llegan hasta el primer y el último valor y que es lo que se conoce como bigotes. Si por casualidad hubiese valores extremos muy separados del resto, los bigotes nunca se dibujan con una longitud superior a una vez y media la caja, en ese caso lo que se hace es colocar los valores extremos como puntos aislados.
Vamos a ver un ejemplo resuelto para que veas como son estos gráficos.
El tema sanitario preocupa siempre a cualquier gobierno. En este caso se quiere hacer un estudio para saber cuál es el término medio de tiempo que se le dedica al paciente en la consulta del médico. Para ello encargan a Mercedes que realice un estudio sobre el número de pacientes que se pueden ver en una hora en un ambulatorio. Los datos que recoge están agrupados en la siguiente tabla.
| nº de pacientes (xi) |
3 |
4 |
5 |
6 |
7 |
8 |
|
nº consultas donde reciben a esos pacientes (fi) |
9 |
17 | 26 | 28 | 15 | 5 |
a) Los datos están más dispersos cuando mayor es el número de pacientes que se atiende en una hora.
b) Como los dos trozos de la caja, dividida por la mediana, son iguales, quiere decir que la dispersión entre el 25% y el 50% es la misma que entre el 50% y el 75%.
c) El recorrido intercuartílico se comprende entre 4 y 6, quiere decir que en la mitad de las horas se atiende entre 4 y 6 pacientes.
Pero el diagrama de caja y bigotes tiene otra ventaja y es que permite comparar fácilmente, dos o más distribuciones de datos correspondientes a la misma variable. Por ejemplo observemos el siguiente dibujo en donde se ha añadido otro estudio realizado en otras consultas.
Según vemos en el que se ha añadido nuevo, aunque la mediana es la misma, pero ahora, la parte izquierda de la caja es mayor que la derecha. Eso quiere decir que los datos entre el 25% y el 50% están más dispersos que entre la mediana y el tercer cuartil, mientras el porcentaje de consultas con pocos pacientes y con muchos es básicamente igual.
Las dos gráficas podían representar el número de pacientes que se atienden en una hora, pero corresponder a especialidades distintas. Por ejemplo la superior corresponder a traumatología y la inferior a medicina general. Lo claro es que en la superior, en general, se dedica más tiempo a los pacientes y por tanto entran menos en una hora.
 |
A una determinada inmobiliaria le están ofreciendo un conjunto de pisos, para que los coloquen a la venta, en una gigantesca urbanización de la ciudad. Dado que ya han vendido otras veces pisos en esa zona y que deben elegir los que van a aceptar, deciden hacer un estudio sobre el nivel de los pisos que han vendido anteriormente en esa zona, para saber si se venden mejor los pisos bajos, los medianos o los altos. Con los datos recogidos en los últimos años han realizado la siguiente tabla de frecuencias.
| Nivel de los pisos vendidos (xi) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| Cantidad de pisos vendidos (fi) |
7 |
5 |
5 |
7 |
8 |
4 |
4 |
2 |
Dibuja el gráfico de caja y bigotes correspondiente a esos datos.
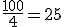 luego Q1 =4
luego Q1 =4
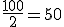 y por tanto Me =5
y por tanto Me =5
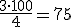 quedando Q3 = 6
quedando Q3 = 6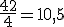 Q1 = 2
Q1 = 2
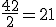 Me = 4
Me = 4
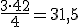 Q3 = 5
Q3 = 5