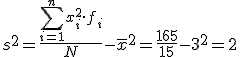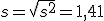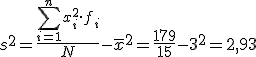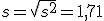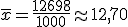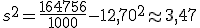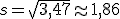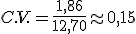2.1 Todos pendientes de la media.

Ya hemos comentado que uno de los estadísticos fundamentales es la media, se utiliza en multitud de ocasiones, muchos elementos se fijan en función de los valores medios que se realizan en estudios y todo parece estar pendiente de ella. Por eso no es de extrañar que los parámetros que vamos a ver en esta sección estén todos pendientes de ella.

Se llaman parámetros de dispersión a una serie de valores que indican lo concentrados o separados que están los datos entre sí y respecto a la media.

Importante

Se llama RECORRIDO a la diferencia entre el valor más pequeño y el más grande que se ha recogido. Nos da una primera idea de si los datos están agrupados o están muy separados, al menos los valores menores y mayores.

Para saber lo separado que están los valores de la media, bastaría restarle a cada valor la media y sumar esas diferencias. El problema es que si lo hacemos, el resultado obtenido es cero. Eso es debido a que, al ser la media el centro, las diferencias por arriba y por abajo se complementan y se anulan. Por eso necesitamos utilizar el valor absoluto.

Se define el parámetro DESVIACIÓN MEDIA como la suma de las diferencias entre los valores y la media, en valor absoluto, dividido por el número total de valores. Si los datos son aislados la desviación media vendría dada por la expresión:

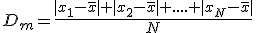
En caso de tablas de frecuencias, la única diferencia es que hay que multiplicar cada diferencia por la cantidad de veces que aparece, es decir, su frecuencia.

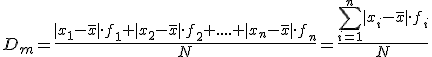
Para practicar.

Para que realices algún ejercicio sobre recorrido y desviación media utiliza el siguiente enlace a los materiales EDAD de matemáticas realizados por el ISFTIC. Tienes la tabla de datos ya preparada y sólo debes calcular esos valores. Ejercítate varias veces.

Enlace al ejercicio

Importante

Para ajustar mejor las diferencias con la media, es corriente elevarlas al cuadrado y de esa forma tenemos un nuevo parámetro. Se define la VARIANZA como la media aritmética de los cuadrados de las diferencias entre los valores de la variable y la media estadística. Suele representarse por s².

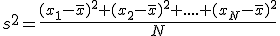
Y para aquellos valores que están agrupados en una tabla de frecuencias basta multiplicar cada diferencia al cuadrado por su frecuencia.

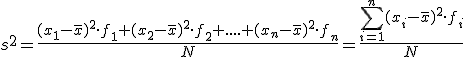
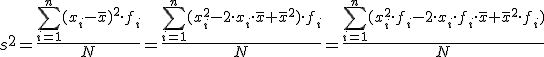
¿Has conseguido recuperar la respiración después del susto de la fórmula anterior? No te preocupes porque hay algún truquito para que puedas realizar esos cálculos sin perder la cordura. Vamos a trabajar un poco en la última fórmula usando el desarrollo del cuadrado de una diferencia que viste en la Unidad 2 cuando trabajamos el álgebra. No te desmayes porque lo que nos interesa es sólo el resultado final.

Si en la segunda expresión descomponemos en tres sumandos y tenemos en cuenta cuanto vale la media, podemos reducir la expresión.

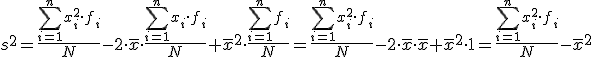
Ahora tranquilízate y fíjate en la expresión final. Nosotros sólo tendremos que calcular la suma de los valores 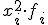, para lo que añadiremos una columna nueva, y después de dividirlo entre el número de valores restarle el cuadrado de la media.

Ejemplo o ejercicio resuelto

Televisión en la que se está viendo un capítulo de la popular serie de ficción "7 vidas"

Vamos a retomar el ejercicio de los televisores que resolvimos en el apartado 1.2. Teníamos la tabla siguiente:

nº de televisores (x_i)	0	1	2	3	4	5
nº de hogares (f_i)	6	30	28	21	9	6

Vamos a calcular su media y su varianza.

La varianza es un estadístico que representa muy bien cuál es el grado de acercamiento o alejamiento, respecto de la media, que tiene la distribución. Pero tiene un problema. Si recuerdas el ejemplo de los espárragos que vimos en el apartado 1.2, la medida de los datos estaba en centímetros y la media también estaba medida en esas unidades. El problema es que si calculamos la varianza, ese estadístico estaría medido en centímetros cuadrados, por lo que es difícil compararlo con la media. Por eso es más usual utilizar otro nuevo parámetro.

Importante

Se define la desviación típica como la raíz cuadrada de la varianza. Se representa, lógicamente, por s.

Utiliza el siguiente applet, tomado de EDAD, para calcular la varianza y, a partir de ella, la desviación típica. Ten presente que con los datos que te aparecen puedes calcular la varianza de dos formas, según las fórmulas que vimos antes con o sin desarrollar el cuadrado de las diferencias entre los valores de la variable y la media.

AV - Reflexión

En el punto 2 hablamos de una posible encuesta a 15 personas sobre el número de veces que se conectaban a Internet y pusimos tres ejemplos, mediante un diagrama, en los que la media era igual a 3. Calcula ahora las desviaciones típicas de los tres casos.

Por último, te planteamos una cuestión, ¿qué distribución era más dispersa, la de los espárragos o la de los televisores que vimos en el punto 1.2? Está claro que no podemos comparar las medias ni las desviaciones típicas, pues no tiene sentido comparar centímetros con número de televisores. Pero sin embargo hay un estadístico que nos permite comparar la dispersión de dos muestras que no se refieren a los mismos elementos. Veámoslo.

Importante

Se define el COEFICIENTE DE VARIACIÓN como el cociente entre la desviación típica y la media.

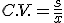
Este parámetro tiene la ventaja de que es un número neutro, es decir, no está referido a ninguna medida. Por ello nos permite comparar datos correspondientes a elementos distintos.

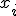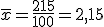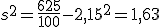
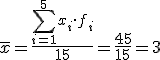
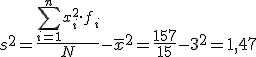
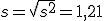Antes de hacer la autoevaluación siguiente, practica con el applet que encontrarás en la siguiente dirección, con lo que puedes comprobar si te ha quedado claro el concepto.

Enlace al applet de Descartes

AV - Reflexión

Espárragos blancos cortados ya sobre un plato

Halla el coeficiente de variación de los datos sobre espárragos con los que trabajaste en el apartado 1.2. Acostúmbrate a redondear a dos decimales las cantidades que utilices.

« Anterior | Siguiente »