1.2 Para muchos datos, mejor la tabla.

Fotografía de la entrada de un centro comercial

Ya sabes calcular los parámetros centrales de un conjunto de datos. Pero, ¿te servirá lo aprendido en todos los casos? Si quieres saber cuál es el gasto mensual medio que tienes de leche en tu casa no hay mucha dificultad. Basta hallar la media de los litros de leche que habéis consumido durante los doce meses de un año. Pero si fueses el director de una empresa con miles de empleados en toda España y quisieras saber cuál es la edad media de tus empleados, la cosa ya se complica.


Si recuerdas el ejemplo de los sueldos de apartado anterior, había tres empleados que cobraban 950 euros. A la hora de hallar la media podíamos sumar tres veces ese valor o calcular 950·3. En el caso de tres no parece muy interesante, pero si se repitiera el mismo sueldo 231 veces la cosa ya varía, no costaría igual tener que sumar 231 veces una misma cantidad en lugar de multiplicarla por 231. Por eso cuando tenemos muchos datos, los cálculos de los parámetros se realizan a través de la tabla de frecuencia.

Icono IDevice Importante

El cálculo de los parámetros de centralización a través de las tablas de frecuencia se realiza de la siguiente forma:

 

MODA: basta fijarse en qué valor de la variable tiene mayor frecuencia absoluta. Recuerda que puede haber dos o más valores cuyas frecuencias sean el máximo valor, en ese caso todos ellos son la moda.

 

Mediana: como los valores están ordenados en la tabla de frecuencias, el procedimiento consiste en calcular la frecuencia absoluta acumulada. Se divide el número total de datos recogidos (N) entre dos y el primer valor cuya frecuencia absoluta acumulada supera a esa cantidad, es el valor mediano. Esto es debido a que si escribiésemos todos los valores ordenados unos detrás de otros, la frecuencia acumulada nos indica hasta qué lugares llegan cada uno de los distintos valores.

 

Si la mitad de N coincide exactamente con el valor de la frecuencia acumulada de un valor estaríamos como en el caso del apartado anterior cuando teníamos un número par de valores. En ese caso la mediana es la semisuma de ese valor y el siguiente.

 

MEDIA: para hallar la media, en lugar de sumar cada valor todas las veces que aparezca, multiplicamos el valor de la variable por la cantidad de veces que aparece (frecuencia absoluta) y la suma de todos esos valores la dividimos entre el número total de valores recogidos. Se aplicaría la fórmula siguiente:


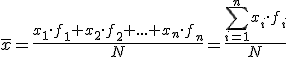
Icono de iDevice Ejemplo o ejercicio resuelto
nº detelevisores nº de hogares
0 6
1 30
2 28
3 21
4 9
5 6

 

Ante la inminente entrada en vigor de la televisión mediante TDT, han encargado a Mercedes hacer un estudio actualizado sobre el número de televisores que tiene cada familia en un determinado barrio de la ciudad. Después de recoger y agrupar los datos, Mercedes ha obtenido la siguiente tabla de valores:

Calcula la moda, la mediana y la media de esos valores.

Si en lugar de valores de una variable discreta, tuviésemos valores de una variable continua, el proceso es muy similar. En este caso en lugar de moda se habla de intervalo modal y, de momento, en lugar de mediana hablaremos de intervalo mediano, aunque en el apartado siguiente veremos como ajustar más ese valor.

 

Para hallar la media únicamente hay que tener en cuenta que se toma como valor xi de la variable el de la marca de clase.

Icono de iDevice AV - Actividad de Espacios en Blanco
Varios botes de espáragos de distintos tamaños

Una empresa envasadora de espárragos blancos quiere estudiar la posibilidad de lanzar al mercado envases de dos tamaños. Uno para productos más grandes, lógicamente de mayor precio, y otro para los elementos más pequeños. Para ello hace un estudio aleatorio del tamaño de espárragos que va envasando obteniendo los siguientes resultados:

Medida en cm.

intervalos

Nº de espárragos

fi

[7,9) 25
[9,11) 172
[11,13) 311
[13,15) 413
[15,17] 79

Completa la tabla con la frecuencia acumulada, la marca de clase y los valores xi·fi. Después calcula los parámetros de centralización y contesta a las siguientes preguntas.

a) El intervalo modal es [ , ).

 

b) El intervalo mediano es [ , ).

 

c) La media, redondeada a dos decimales vale .

  

En el siguiente applet puedes practicar el cálculo de la media, que quizás sea el más complicado y utilizado de los tres parámetros. Está tomado, como varios de los anteriores, del material EDAD, creado por el ISFTIC para la enseñanza a distancia. Puedes practicar varios ejemplos tanto para variables discretas como continuas. Para cambiar de un tipo a otro pulsa el botón Discreta/Continua y para pasar a otro ejemplo el de Genera.

Icono IDevice Curiosidad
Hemos comentado que la mediana y la media no tienen sentido en las variables cualitativas, pero a veces, para poder sacar esa información incluso en datos no numéricos, lo que se hace es codificar las respuestas. Por ejemplo, te habrás encontrado a veces en encuestas en la que al preguntar sobre cuál es tu grado de satisfacción con un determinado servicio te habrán pedido que elijas un número del 1 al 5, en donde el 1 significa nada satisfecho y el 5 muy satisfecho. De esa forma se evalúan los datos numéricos correspondientes y se pueden hallar todos los parámetros.

« Anterior | Siguiente »