1.1 Lo más básico.
 |
Hay conceptos estadísticos que seguro que utilizas muy a menudo, aún sin darte cuenta. Si tienes tantos hermanos o hermanas mayores que tú, que menores, entonces tú eres el o la herman@ median@. Si utilizas algo que está de actualidad, es porque estás a la moda, es decir, te relacionas con lo que más gente usa en esos momentos. Si te gusta salir los fines de semana de marcha, seguro que unos días gastarás más que otros, pero si quieres saber cuál es el gasto medio al mes deberás calcular la media estadística de los gastos de cada fin de semana. Pues estos tres conceptos tan elementales son los que vamos a desarrollar en esta sección.
Se llaman parámetros de centralización aquellos valores en torno a los cuales están agrupados los datos. Básicamente son los valores centrales del conjunto de valores recogidos y representan, de forma global, a toda la población o la muestra.
Importante
La moda es el único estadístico que puede utilizarse con cualquier tipo de variable. En concreto es el único parámetro que tiene sentido calcular en las variables cualitativas.
Tiene además la particularidad de ser el único parámetro estadístico que puede tomar más de un valor. Por ejemplo, una familia muy numerosa, con ascendencia de partos múltiples tiene 6 hijos cuyas edades son 3, 3, 6, 10, 10, 14. Entre esos datos, la moda correspondería a los valores 3 y 10 ya que ambos se repiten dos veces.
AV - Actividad de Espacios en Blanco
Importante
Si suponemos que los datos están ordenados numéricamente de menor a mayor, la MEDIANA es el valor que está en el centro, es decir, el valor que tiene por delante la mitad de los valores y por detrás la otra mitad. La representaremos por Me.
 |
Si el número de valores que tenemos es impar, la mediana será el que ocupe el valor central. Por ejemplo, si el número de personas que viven en los distintos pisos de un bloque de viviendas son: 2, 2, 2, 3, 4, 4, 5, 5, 6, la cantidad mediana de personas que viven en esos pisos sería de 4 personas.
Sin embargo, si el número de valores de los que disponemos fuese par, entonces la mediana es la semisuma de los dos valores centrales. Y no importa que obtengamos un valor decimal, aunque parezca no tener sentido en el contexto. Si en el ejemplo anterior hubiese una vivienda más con tres personas, entonces los valores centrales serían el 3 y el 4, por lo tanto, la mediana sería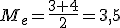 
AV - Actividad de Espacios en Blanco
- El sueldo que correspondería con la mediana sería euros.
- Si consideramos también el sueldo del gerente, que cobra 2500 euros, entonces la mediana de esos valores sería un sueldo de euros.
Importante
La MEDIA es el valor promedio del conjunto de valores que estamos trabajando. Suele representarse por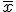 
. Suele considerarse a la media como el centro de gravedad de la distribución de valores y, como veremos, no tiene porqué estar exactamente en la mitad.
Se calcula sumando todos los valores obtenidos y dividiendo entre el número total de datos. Si los datos que tenemos son x1, x2, x3, .... hasta el valor xN entonces la media vendría dada por la expresión.
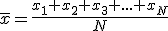
La media equivale al valor que obtendríamos si reuniésemos todo el valor completo de la variable y la repartiésemos a partes iguales entre todas las observaciones que hubiésemos hecho. Te pondremos un ejemplo. Si sumamos los sueldos de todos los empleados tendríamos 805+950+950+950+1200+1200+2100 = 8155 € y si ahora calculamos la media obtendríamos:
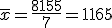
Si suponemos que todos los empleados cobrasen igual, sería precisamente ese valor medio, ya que la suma de todos los sueldos valdría lo mismo: 805+950+950+950+1200+1200+2100 = 8155 = 1165 · 7.
AV - Reflexión
Curiosidad
Para comprobar como afectan los valores extremos puedes utilizar el applet que encontrarás en el siguiente enlace. Hay siete valores representados, que puedes modificar pulsando sobre los puntos rojos y moviéndolos con el ratón. Al mover cualquiera de los valores se actualizará la media y la mediana automáticamente. Aunque el applet está en inglés no creemos que tengas problemas para utilizarlo, sólo advertir que la media es mean y la mediana es median.
Puedes probar colocando los valores 340, 350, 360, 370, 380, 390 y 400 y, a continuación, mover el primer valor de 340 hasta valores menores que 50 para ver el efecto. Mueve después distintos puntos para ver el efecto sobre la media y la mediana.
|
Para Practicar
Puedes realizar algunos ejemplos de cálculo de moda, mediana y media en el siguiente applet de descartes tomado de los materiales EDAD. Utilizando el botón de Comprobar puedes ver si tienes bien los cálculos, y cuando lo pulses se transforma en la opción de Otro ejemplo. |