2.1 Cuando los datos son muy reservados.
 |
¿Eres una persona aficionada a la lectura?, ¿posees muchos libros en tu casa o en tu trabajo? Aún en el caso de que no te ocurra esto, piensa en una biblioteca. Hay multitud de libros y para poder tenerlos organizados de forma que sean fácilmente accesibles, deben estar ordenados. Una de las primeras ordenaciones es agruparlos por los que son del mismo género. Algo parecido a lo que se hace con los libros es lo que vamos a hacer nosotros con los datos recogidos en una encuesta o por cualquier otro medio.
Lo que veremos en este apartado y el siguiente valdrá para las variables cualitativas y las cuantitativas discretas. En el punto 2.3 veremos que pasa con las variables cuantitativas continuas.
Se llama tabla de frecuencias a una tabla en la que se relacionan los distintos resultados de la variable con la cantidad de veces que han aparecido dichos resultados.
Los conceptos que vamos a reflejar en las tablas van a tener una representación que es necesario que conozcas. Ya hemos definido en la parte anterior qué se entiende por variable estadística: lo que estudiamos de la población. Vamos a representar la variable que se está estudiando por la letra x. Si suponemos ordenados de alguna manera los posibles valores de esa variable, llamaremos x1 al primer valor, x2 al segundo y así sucesivamente. En general, la columna donde vamos a colocar esos resultados la encabezaremos por el símbolo xi para indicar que están todos los valores, cada uno con su subíndice u orden correspondiente.
Se llama frecuencia absoluta al número de veces que aparece un determinado resultado de la variable estadística entre todos los datos que se han recogido. Vamos a representarla genéricamente por la letra f.
Si hemos entrevistado a 500 personas, de las cuales 227 han sido hombres y el resto mujeres, la frecuencia absoluta del resultado Hombres sería 227 y del resultado Mujeres sería 273.
| |
Al lado tienes una tabla de frecuencias donde se han recogido el color de pelo de 100 personas y se han agrupado según su frecuencia absoluta. Como puedes apreciar lo único que hay que hacer es poner los resultados posibles y al lado la cantidad de veces que se han recogido esos resultados.
 |
El número total de elementos recogidos, que debe coincidir con la suma de todas las frecuencias absolutas, suele representarse por la letra N.
|
Para practicar
Practica con el ejemplo siguiente tomado de los materiales EDAD para 3º de ESO elaborados por el ISFTIC y el CIDEAD. Cada vez que pulses el botón Genera te aparecerá una distribución distinta de bolas para que practiques.
En la página web de Descartes puedes encontrar otros ejemplos para practicar, accede desde el enlace AQUÍ.
|
Una pequeña empresa de seguros está realizando un estudio de los accidentes de tráfico que han tenido sus asegurados en el último mes, con intención de revisar el precio de las primas. Ha elegido aleatoriamente 40 asegurados y obtenido los siguientes datos.
2, 1, 3, 0, 1, 0, 0, 3, 0, 1, 4, 2, 1, 0, 0, 0, 1, 1, 2, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 1, 3, 2
Esos datos se han agrupado en la siguiente tabla de frecuencias. Rellena los huecos correspondientes.
| xi |
fi |
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 |
Se llama frecuencia relativa de un resultado al cociente entre su frecuencia absoluta y el número total de datos que se han recogido. Vamos a representarla por h. En ese caso la frecuencia relativa se calcularía como 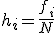 .
.
El tanto por ciento de un resultado de la variable se halla multiplicando la frecuencia absoluta por 100 y dividiendo por el total o, directamente, multiplicando la frecuencia relativa por 100.
La frecuencia relativa es, en el fondo, una proporción. Es decir, cuando hablamos de la frecuencia relativa de los pelirrojos en un conjunto de personas es el cociente entre el número de pelirrojos respecto del total. Esto lo puedes ver con una sonrisa en el siguiente vídeo argentino.