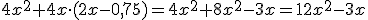3. Trabajando con expresiones
 |
Algunas de las expresiones que has visto pueden parecerte un poco complicadas y seguro que te estás preguntando, ¿esto no se puede expresar más fácilmente? Vas a ver que sí.
En ocasiones es necesario agrupar de alguna manera distintas expresiones. Las reglas para realizar estas agrupaciones son equivalentes a las utilizadas para operar con los números. Por ejemplo, ya hemos utilizado anteriormente la fórmula que expresa el espacio en función de la velocidad, e=v·t. La velocidad que alcanza un cuerpo que cae viene dada por v=g·t, donde g es un valor constante que se llama constante de aceleración y está relacionada con la fuerza de la gravedad aquí en la Tierra, vale 9,8 m/seg2. Para calcular el espacio que recorre un objeto que cae libremente utilizaríamos la expresión
que es la fórmula que viste en el vídeo del apartado 2.
Una de las diferencias fundamentales en las operaciones entre expresiones algebraicas es que no siempre podemos agrupar los valores en uno solo, únicamente podemos hacerlo cuando tengamos expresiones que sean equivalentes, que son aquellas en las que la parte formada por las letras es exactamente igual, es decir, se diferencian sólo en el coeficiente numérico que forma parte de la expresión.
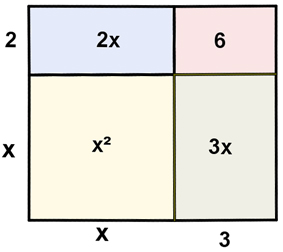 |
Vamos a ver un ejemplo utilizando una visualización geométrica. Consideremos la siguiente figura de la que queremos hallar su área. Para ello podemos hacerlo de dos maneras distintas. Si consideramos las medidas totales de los lados que serían x+3 y x+2, entonces su área sería:
(x+3)·(x+2)
Pero si consideramos los rectángulos que lo forman también podríamos calcular su área como:
x2+3·x+2·x+6
Para ver que ambas expresiones son iguales, ve pulsando en la siguiente presentación.
Quizás recuerdes el truco de magia con que comenzamos el tema. En el punto 1.1 viste que expresión algebraica correspondía a las operaciones que había que hacer. Ahora ya estás en disposición de comprobar por qué el truco se verifica siempre. Para ello haz clic sobre la ventana siguiente.
 |
Juan está pensando en comprarse un televisor nuevo de plasma y está diseñando un mueble para colocarlo. Ha pensado en las siguientes características:
Quiere que la relación entre la altura y la anchura esté en la relación 3 a 4.
La tercera parte superior la va a dedicar a libros y una serie de adornos. Quiere dividirla en cuatro partes iguales.
Debe dejar un hueco de 75 cm. para colocar el televisor junto con algún jarrón, y la parte inferior restante la dividirá en tres partes donde colocará unas puertas para guardar papeles, DVD y otros elementos.
Ha realizado un esquema como el de la imagen en donde ha tomado las longitudes de los lados como 3x y4x para que le resulte más fácil el reparto.
Ahora queremos encontrar las expresiones algebraicas que corresponden a las siguientes cuestiones.
Una de las fábricas textiles que surte a la tienda de Juan fabrica trajes completos. La empresa tiene una serie de gastos fijos por el alquiler del local, transporte y personal de 8.000 euros. Por otro lado, tiene unos gastos de 30 euros en concepto de material para cada traje.
La empresa ofrece los trajes a las tiendas a un precio de 100 euros.
Escribe la expresión que daría la ganancia que obtiene la fábrica al fabricar y vender x trajes.
|
a) 70·x - 8000
| |
|
b) 8000 - 70·x
| |
|
c) 100·x + 8030
|
En el siguiente Applet de Descartes creado por Esther Pérez Fernández, tienes figuras formadas por varios polígonos y queremos escribir la expresión que corresponde al área de cada una de dichas figuras. Para pasar de una a otra basta que pulses sobre los triángulos azul y rojo de la casilla Área nº.
En las opciones siguientes tienes las expresiones de las áreas de las 5 combinaciones que aparecen. Debes escribir en los huecos a qué número de área corresponden.
a) x2+12x+8 área nº b) 2x2+10x+6 área nº
c) 2x2+4x+4 área nº d) x2+8x+5 área nº
e) x2+12x+4 área nº
Existen muchas operaciones que aparecen regularmente al trabajar con expresiones algebraicas e incluso hay fórmulas que nos permiten agilizar los cálculos. Quizás las más conocidas sean los productos notables, que son expresiones que nos permiten hallar rápidamente el cuadrado de una suma o de una diferencia, por ejemplo.
En la siguiente dirección te hablan de esos elementos y tienes un pequeño taller interactivo donde puedes practicar esos elementos.
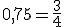 tendríamos la operación
tendríamos la operación 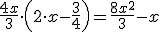
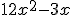 .
.