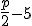1.1 Paso del lenguaje cotidiano al simbólico

 Montaña con calcetines

 

Juan está en su tienda haciendo recuento de los calcetines que tiene en exposición. Ha anotado en su cuaderno lo siguiente: 3 b + 7 n + 5 m, ¿qué crees que estará representando con ello? Seguro que te resultará más fácil entenderlo si te comentamos que tiene en ese momento 3 pares de calcetines blancos, 7 negros y 5 marrones.

 

El camino a recorrer entre el lenguaje cotidiano y el algebraico no es tan complicado como puede parecer. En pocas palabras, consiste en sustituir elementos de diversa índole por símbolos. Ya hemos visto anteriormente que lo hacemos continuamente en la vida diaria.

 

Has visto en el primer párrafo que con unos pocos símbolos puede tener la información completa sobre los calcetines en exposición. Como veremos más adelante, si sustituimos las letras que aparecen por el precio de cada par de calcetines, puede saber exactamente cuánto puede ganar si los vende todos.

 

Icono de iDevice Ejemplo o ejercicio resuelto
Juan está esperando un pedido de blusas de la nueva temporada, de momento no sabe qué precio de venta asignarles. Por ello representa ese precio por el símbolo p.
¿Cómo expresarías el valor de tres blusas?

¿Y el valor de un pantalón que vale 10 euros más que la blusa?

Un pañuelo cuesta cinco euros menos que la mitad de una blusa, ¿qué expresión tendría su precio?

Si la blusa se ha rebajado un 10%, ¿cómo expresarías el nuevo precio de la blusa?

Icono IDevice Actividad
Como has podido ver en el ejercicio resuelto, una expresión algebraica es un conjunto de letras y números unidos mediante operaciones aritméticas.

Icono de iDevice Ejemplo o ejercicio resuelto

Vamos a aplicar la simbolización algebraica al truco de magia que hemos visto antes. Vamos a seguir los pasos que nos pedía el truco y ver qué expresión obtenemos. Como el número que habías pensado no lo conozco, lo voy a representar por un símbolo, en este caso la letra x.

 

Lenguaje cotidiano
 Lenguaje algebraico
Piensa un número
 x
súmale 3
 x+3
multiplica el resultado por 2
 (x+3)·2
súmale 4
 (x+3)·2+4
divide lo obtenido por 2
 [(x+3)·2+4]/2
súmale 6
 [(x+3)·2+4]/2+6
réstale el número que pensaste
 [(x+3)·2+4]/2+6-x
súmale 5
 [(x+3)·2+4]/2+6-x+5

 

 

Recuerda la importancia de la jerarquía de operaciones y acuérdate de colocar los paréntesis cuando sean necesarios. En general, siempre que vayas a multiplicar o dividir una expresión en la que aparezca una suma o una resta, ésta debe ir entre paréntesis.

Para practicar:

Si quieres practicar está relaciones entre el lenguaje usual y el simbólico, antes de pasar a la Autoevaluación, puedes visitar la página a la que te lleva el siguiente enlace. En ella hay algunas actividades con evaluación automática, creadas con Hot Potatoes.

Practica sobre los cinco  primeros tests. El resto aún no lo hemos aprendido. 

Paso al lenguaje algebraico

AV - Pregunta de Selección Múltiple
De camino hacia la tienda, Juan para a tomarse un café en el bar en el que suele desayunar todos los días. Paga con un billete de 10 euros y recoge la vuelta sin fijarse cuánto le ha costado. A continuación, hace una parada en un quiosco y se gasta 3,50 en una revista de moda. Si llamamos c a lo que se ha gastado en el bar, selecciona todas las opciones que pueden expresar la cantidad de dinero que le quedan de los 10 euros.
a) 10-c-3,5
b) 10-(c-3,5)
c) 10-(c+3,5)
d) c+3,5-10



Veamos ahora unas preguntas sobre edades.
Icono de iDevice AV - Actividad de Espacios en Blanco

A Juan no le gusta que la gente sepa su edad, así que el siempre responde que tiene "a" años. Escribe en los espacios siguientes las edades de sus familiares y amigos.

 

Ten en cuenta que no es necesario escribir el símbolo del producto, y para la división utiliza el símbolo /.

RELACIÓN CON JUAN EXPRESIÓN
La edad de su amigo Felipe que tiene 3 años más que él
La edad de su hermana pequeña si tiene la mitad de edad que él más 5 años
La edad de su padre al que le faltan 7 años para tener el doble que él.
La edad de su amiga Luisa, que si se suma con la edad de Juan, da 75 años.

 

  

En la vida estamos rodeados de Geometría y en muchas ocasiones nos encontramos con expresiones algebraicas como las que aparecen en la siguiente autoevaluación.
AV - Pregunta Verdadero-Falso
A continuación, tienes una serie de polígonos y queremos que nos digas si las expresiones que los acompañan corresponden a su perímetro.


El perímetro de este cuadrado es 4·x

Verdadero Falso


El perímetro del hexágono es 6·b

Verdadero Falso


Ahora el perímetro vale 3·a + 2·b

Verdadero Falso


El perímetro total de la figura es 2·b+14

Verdadero Falso     
Icono de iDevice AV - Reflexión

Ahora te lo vamos a poner un poco más difícil.

Imagina que vas a la tienda de Juan y que te entrega una factura que pone 3·p+5·4, ¿serías capaz de crear una frase que correspondiera a esa expresión?

« Anterior | Siguiente »