3.3. Buscando solución a los problemas diarios
|
|
Planet, de Southernpixel,
|
¿Sirven las ecuaciones en el mundo que nos rodea?
Ya sea consciente o inconscientemente, resolvemos problemas del día a día por medio de ecuaciones: al comparar productos en el mercado, cuando hacemos viajes, en nuestras cuentas bancarias y al buscar una nueva compañía telefónica. Incluso para hacer la foto de la izquierda, se han usado ecuaciones.
Vamos a ver algunos tipos de problemas que se resuelven con ecuaciones de primer o segundo grado con una incógnita. Evidentemente no todos los problemas tienen solución, ni todos los podemos solucionar con las herramientas que tenemos hasta este momento, pero ya verás que tan sólo con lo que hemos visto, ya se pueden resolver bastantes situaciones.
Ejemplo o ejercicio resuelto
En mi compañía telefónica me ofrecen una tarifa reducida y una tarifa plana para el móvil. Las condiciones de cada una son las siguientes:
| Concepto |
Tarifa Reducida |
Tarifa Plana |
|
Establecimiento
|
15 cént. | 15 cént. |
|
Llamadas a móviles
|
3 cént./min. | 19,9€/mes |
|
Llamadas a móviles
|
30 cént./min | 18 cént./min |
Mirando las facturas de los últimos meses, he visto que suelo hablar el doble de tiempo con los móviles de mi compañía que con los que son de otra. ¿Cuánto tiempo tengo que hablar para que las dos tarifas me salgan por el mismo precio?
Como el establecimiento de llamada es el mismo en las dos tarifas, y podemos suponer que haré el mismo número de llamadas con ambas, no vamos a considerar este dato. Ten en cuenta que todos los valores los pasaremos a euros. Vamos a plantear el problema paso a paso:
a) Si x es el número de minutos que hablo al mes con los móviles de otras compañías, ¿cuánto me gastaré al cabo de un mes con la tarifa reducida?
AV - Actividad de Espacios en Blanco
En la actualidad tengo unos ahorros de 3100€, que me gustaría aumentar a 4340€ en cuatro años para poder realizar ciertas obras. ¿A qué interés simple anual debo invertirlo para obtener dicho capital?
Utilizaremos la fórmula de interés simple: CF=C0(1+0,01it), donde CF es el capital final, C0 el inicial, i es el interés y t el tiempo.
Sustituye los datos del problema en la fórmula: = (1+0,01i· )
Resuelve la ecuación para despejar i. Solución: i = % anual.
AV - Actividad de Espacios en Blanco
Para cambiar el suelo de la cocina tengo dos opciones:
- Las baldosas Terra miden 30 cm de ancho y 40 cm de largo, y cada una tiene un precio de 1,10€.
- Las baldosas Azur miden 20 cm de ancho y 50 cm de largo, y su precio es de 0,95€ por baldosa.
¿Qué superficie tiene la cocina si sé que con las baldosas Terra necesitaría 40 menos que con la Azur? ¿Con qué baldosa me saldría más barato?
a) Si x es el número de baldosas Azur que necesito, del modelo Terra me harán falta baldosas.
b) La superficie que cubro con x baldosas Azur será de cm2. La superficie con baldosas Terra será (x- ) cm2.
c) Como con ambas cubro toda la cocina, plantea la ecuación y calcula el número de baldosas de cada tipo que necesito:
Baldosas Terra:
Baldosas Azur:
d) El precio más económico lo obtengo con las baldosas , que me costaría en total €
AV - Actividad de Espacios en Blanco
En Física, el espacio que recorre un cuerpo que se mueve en linea recta sin variar la velocidad, viene dado por la fórmula e = e0+vt, donde t es el tiempo y e0 es el espacio inicial.
Si en ese movimiento lo que permanece constante es la aceleración, entonces tenemos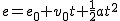 
, donde v0 es la velocidad inicial, a es la aceleración y t el tiempo.
Si Fernando Alonso entra en una recta del circuito a una velocidad de 15m/s con una aceleración de 6m/s2, ¿cuánto tiempo tardará en recorrer la recta de 450m? (puedes suponer que e0=0).
Solución: Tarda segundos.
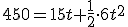
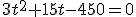
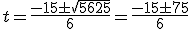
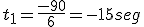(no es válida por ser un tiempo negativo)
