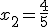3.2. Ecuaciones de segundo grado y racionales
 |
| Día 110 de Freddy the Boy, CC by 2.0 |
Una ecuación será de segundo grado si tiene algún término en x2.
Una vez que hayamos quitado paréntesis, denominadores y la ecuación se haya quedado lo más simplificada posible (siguiendo los pasos 1 a 3 del apartado anterior), nos quedará una ecuación de la forma ax2+bx+c=0, donde a, b y c son números reales.
Las ecuaciones de segundo grado pueden tener dos, una, o ninguna solución. Para resolverlas, usaremos la siguiente fórmula:
Veamos un ejemplo: 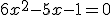
En este caso, será a = 6, b = -5 y c = -1. Si lo sustituimos en la fórmula, nos queda:
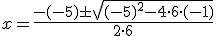
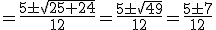
Obtenemos dos soluciones, una operando con + y otra con -
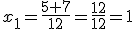 y
y 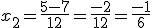
- Las ecuaciones de segundo grado en las que b o c son iguales a cero, se llaman incompletas. Se pueden resolver por la fórmula que hemos visto, pero existen métodos más sencillos en estos casos. Si quieres saber cómo se resuelven, consulta la web Edumates.
- ¿Te interesa saber de dónde sale la fórmula de resolución de las ecuaciones de segundo grado? En El Blog de Ed encontrarás la respuesta.
En la fórmula hay una raiz cuadrada que va a ser la que determine el número de soluciones de la ecuación. La expresión a la que calculamos la raiz, b2-4ac, se llama discriminante. Tendremos los siguientes casos:
- Si b2-4ac > 0: La raiz existe, y por lo tanto la ecuación tendrá dos soluciones, una operando con + y otra con -.
- Si b2-4ac = 0: La raiz vale 0 y la ecuación tendrá una única solución, x = -b/2a.
- Si b2-4ac < 0: La raiz no existe y la ecuación no tiene solución.
- Quitamos paréntesis:
- Pasamos todos los términos al mismo miembro:
- Usamos la fórmula de resolución:
Resuelve las siguientes ecuaciones y completa los huecos. Si tiene una única solución, escríbela repetida en cada hueco. Si no tiene solución, escribe no en cada hueco. Los huecos con una barra / entre ambos indican una fracción.
- x2+2x+1=0 tiene solución y
- x2+5x+7=0 tiene solución y
- (2x-1)2=5x-1 tiene solución y /
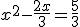 tiene solución
y
/
tiene solución
y
/
Por último, veamos las ecuaciones racionales, que son aquéllas en las que la incógnita aparece en algún denominador. Básicamente se resuelven igual que las que vimos con fracciones, pero teniendo en cuenta que hay que hacer el mínimo común múltiplo también con los denominadores que contengan expresiones algebraicas.
También se pueden resolver multiplicando ambos miembros por el producto de todos los denominadores. Una vez resuelta la ecuación, es importante comprobar las soluciones, pues no todas serán válidas.
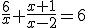
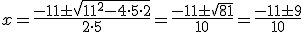
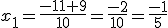 y
y 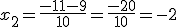
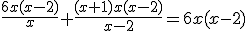
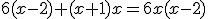
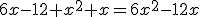
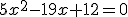
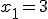 y
y