1.2. Recta real
Una herramienta muy útil para exponer de manera secuencial los hechos importantes que dieron forma a un suceso histórico, es utilizar una línea del tiempo. Por ejemplo, observemos la siguiente imagen en donde se presentan varios hitos importantes de la aventura espacial que desembocaron con la llegada del hombre a la Luna.
 |
|
Las dos imágenes corresponden a Luna 9 landing cápsule y Surveyor 3 Apollo 12, tomadas de Wikipendia con licencia Dominio Público
|
Del mismo modo que una línea del tiempo facilita la visión sobre un acontecimiento histórico, representar los números reales en una recta, ayudará a entender mejor determinadas propiedades de este conjunto numérico, como pueden ser el orden y la distancia entre ellos.
AV - Reflexión
Actividad
Llamaremos recta real a una recta graduada en la que se fija como origen el número 0, se determina una unidad y se van colocando los números positivos hacia la derecha y los negativos a la izquierda.
Cada número real ocupa un lugar en la recta real, y viceversa, cada punto de la recta real está ocupado por un número real.
En la siguiente imagen, aparecen representados varios números reales.
 |
 |
|
TrainRaisPresblog por Julie70, CC by-nc-sa 2.0
|
En el Importante anterior, podemos ver que 
es menor que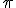 
, o que -2,3 es mayor que 
. Es decir, representar números en la recta real permite ordenar de una forma muy gráfica dichos números.
Recuerda los signos que se utilizan en matemáticas para expresar el orden: <, >, 
y 
. Por ejemplo, escribimos 
o 
.
AV - Reflexión
En la siguiente escena de Descartes, creada por el profesor Miguel Ángel Cabezón, es posible representar en la recta real números racionales expresados por una fracción, por ejemplo 7/3 u 8/11, y raíces de números reales, que escribiremos sqrt(r), donde r es el número real. Por ejemplo sqrt(3) ó sqrt(11).
El número real que deseemos representar lo escribiremos en la ventana que está a la derecha de Número. También podemos usar el control zoom para acercarnos o alejarnos de la recta real.
Ayúdate de esta escena para ordenar y representar de forma aproximada los siguientes números:
, 
, 
y 
< 
Objetivos
En la autoevaluación anterior hemos representado números reales en la recta real de forma aproximada. En los siguientes enlaces al Proyecto EDAD del Ministerio de Educación, se explica cómo podemos representar con más exactitud los números racionales escritos como fracción, y los irracionales que vengan expresados como raíz cuadrada de un número natural que no sea cuadrado perfecto.
1. Racionales
2. Irracionales