1.1. Decimales, racionales, irracionales: Reales
La Tierra donde vivimos, la Luna que gira a nuestro alrededor, el balón alrededor del que giran la mirada y el ocio de millones de aficionados en todo el mundo, y multitud de objetos tanto de la naturaleza como creados por el ser humano tienen forma esférica, o utilizando un lenguaje coloquial, son redondos.
La rueda, sin duda uno de los grandes inventos de la humanidad, es una circunferencia. El uso de la rueda para el transporte, para girar en las norias y elevar el agua o batir las semillas en los molinos. No nos puede extrañar que desde muy pronto el ser humano se fijara en la circunferencia y se preguntara por la relación que existe entre el perímetro y el diámetro. De esa relación surgió uno de los números más famosos y conocidos por todas las civilizaciones: π.
Para convencerte de que es cierto lo que hemos dicho, disfruta de este vídeo.
Como has podido comprobar, a lo largo de la historia de la humanidad ha existido la necesidad de conocer el desarrollo decimal de π. Algunas han sido aproximaciones muy pobres, como la que aparece en los textos bíblicos. Pero otras, y sobre todo a partir del siglo XVI con el desarrollo del cálculo infinitesimal, muy buenas .
La siguiente autoevaluación nos va a servir para repasar algunas de estas aproximaciones.
AV - Actividad de Espacios en Blanco
a) La peor aproximación de π corresponde a Salomón, en el 900 a.c., que lo expresa como la fracción / .
b) Hacia el 1.700 a.c., en Babilonia, se escribía π como la fracción 25/8, que es igual a , .
c) En Egipto, allá por el 1.650 a.c., se pensaba que π podía ser igual a ( / )2= 3,16.
d) Arquímedes, ya en el 250 a.c., puso a π entre los siguientes valores: 3, > π > 3, .
e) El sabio chino Chung Chih, en el siglo V de nuestra era, lo aproximó como / = 3,141592.
Todas las aproximaciones que se pueden dar de π vienen escritas como números decimales con una cantidad determinada de cifras decimales o una fracción, es decir, un cociente de números enteros.
Pero por muchas cifras que se conozcan, ninguna aproximación será exactamente π. Porque su desarrollo decimal no sigue ninguna regla. Igual ocurre con Φ, la forma en que aparecen sus decimales no cumple ninguna norma.
Aquí tienes escrito Φ con 30 cifras decimales. ¿Sabrías decir cuál es la que ocupa el lugar 31?
1,618 033 988 749 894 848 204 586 834 365 ...
Actividad
Los números irracionales son aquellos que poseen un desarrollo decimal con infinitas cifras decimales no periódicas. Un número irracional nunca se puede expresar como una fracción o cociente de números enteros. Por ejemplo π,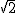 
y en general cualquier raíz cuadrada de un número natural que no sea cuadrado perfecto, son números irracionales.
Los números racionales son aquellos que tienen un desarrollo decimal finito, o infinito periódico. Es decir, en algún momento las cifras decimales se repiten. Un número racional siempre se puede escribir como una fracción o cociente de números enteros. Por ejemplo, la aproximación tan buena que dio Francoise Vieta de π 3,1415926536 o la de los chinos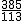 
, son números racionales.
Al conjunto de los racionales e irracionales es lo que denominamos números reales. Que para simplificar se expresa con una R.
Ejemplo o ejercicio resuelto
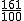. Indica a qué conjunto numérico pertenece cada uno de los números anteriores, es decir, si son racionales o irracionales.
Pre-conocimiento
 |
| Burgos´09 Covarrubias libro de música medieval, de ferlomu, CC by-nc-sa 2.0 |
Los nombres de racionales e irracionales viene de las matemáticas griegas. Racional tiene su origen en razón, que no tiene otro sentido más que proporción o división. Un número racional es el que se puede expresar como proporción de dos números enteros. Por tanto, un irracional es el número que no se puede escribir como el cociente de dos enteros.
Para entender mejor la diferencia entre racionales e irracionales, veamos la imagen que propone el profesor Fernando Corbalán: "si asignamos un sonido a cada cifra y hacemos sonar los decimales de un racional, escucharíamos una melodía que se va repitiendo, como el estribillo de una canción. En el caso de los números irracionales las notas sonarían sin ton ni son, y no podríamos obtener jamás una melodía".
AV - Pregunta Verdadero-Falso
es racional
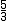es racional.