2. Nada es exacto
 |
|
Marani de onicófago, |
Cuando vamos a comprar frutas o verduras y pedimos un kilo o tres cuartos de algún producto, si nos fijamos bien en la cantidad que marca la balanza, casi nunca el frutero coloca la cantidad exacta de la mercancía que hemos solicitado. "Pasa un poco del kilo", nos dice el comerciante; o "le faltan 35 gramos para los tres cuartos".
"Nos vemos a las siete y media en la puerta del cine", y nadie llega a la hora exacta a la cita. Muy pocos llegarán unos minutos antes, y casi todo el mundo con algo de retraso.
Si lo piensas bien, existen muchas situaciones en nuestra vida cotidiana en donde utilizamos los números de manera aproximada. Lo mismo ocurre con los números decimales, ante la imposibilidad de operar con ellos utilizando todo su desarrollo decimal lo que hacemos es aproximarlos y quedarnos con tan sólo unas cuantas cifras de dicho desarrollo. Además, en la vida real no es necesaria mucha precisión, basta con 2 ó 3 decimales.
Actividad
Dos maneras de aproximar un número decimal son el truncamiento y el redondeo.
Una aproximación por truncamiento consiste en suprimir todos los decimales a partir de una cierta cifra.
Es decir, si el truncamiento se hace a la cuarta cifra decimal, a partir de ella suprimimos el resto del desarrollo decimal. Por ejemplo, aproximar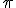 
como 3,1415 es realizar un truncamiento a la cuarta cifra decimal.
Una aproximación por redondeo consiste en suprimir todos los decimales a partir de una cierta cifra, teniendo en cuenta que si la primera cifra que se suprime es mayor o igual que 5, se aumenta en una unidad la última cifra de la aproximación.
Por ejemplo, si queremos aproximar por redondeo a la cuarta cifra decimal los números 2,63636363... y Φ= 1,618033... obtendríamos 2,6364 y 1,6180 respectivamente.
AV - Actividad de Espacios en Blanco
Recordemos las diez primeras cifras decimales de nuestro querido número Φ= 1,6180339887.
Completa en la siguiente tabla los espacios en blanco correspondiente a las aproximaciones de Φ que se indican.
| Truncamiento | Redondeo | |
| a la 3ª cifra decimal |
1, | 1, |
| a la 6ª cifra decimal | 1, | 1, |
| a la 8ª cifra decimal |
1, | 1, |
Puede ser que te hayas dado cuenta que al aproximar un número por truncamiento, obtenemos siempre un número más pequeño. Cuando esto ocurre, es decir, la aproximación es menor que el número aproximado, la llamaremos una aproximación por defecto. En caso contrario, cuando es mayor, se dirá que es por exceso.
Un aspecto muy importante que hay que tener en cuenta en el proceso de aproximar un número, es el control del error cometido. Veamos con un ejemplo, qué queremos decir con esto.
Ejemplo o ejercicio resuelto
 |
| Pastillas de juanpol, CC by 2.0 |
Veamos un caso práctico. En el prospecto de unas cápsulas se indica que cada gramo del medicamento contiene 0,00285 gramos de ácido bórico y 0,00015 gramos de tetraborato de sodio.
En un control de calidad farmacéutico, se toma una muestra de una de las cápsulas y se detecta que cada gramo de la medicina contiene 0,0031 gramos de ácido bórico y 0,00013 gramos de tetraborato.
a) En uno de los casos el error es por exceso, supera a la cantidad fijada, y en el otro es por defecto, está por debajo. ¿cuál es uno y cuál es el otro?
b) ¿En cuál de los dos componentes la diferencia entre la cantidad indicada en el prospecto y la detectada en el tubo es mayor?
Actividad
Se denomina error absoluto a la diferencia entre el valor real de un número y su aproximación. Se suele tomar el valor absoluto de dicha diferencia.
Los errores absolutos cometidos en las muestras detectadas de la pomada son 0,000250 para el ácido bórico y 0,00002 en el tetraborato.
AV - Reflexión
En la siguiente escena creada con Geogebra aparecen un número y una aproximación a él. Halla el error absoluto de varias aproximaciones y comprueba si tus cálculos son correctos. Para generar otro número y otra aproximación a él, pulsa sobre el icono de la parte superior derecha de la escena.
El error absoluto de una aproximación puede resultar a veces engañoso si lo que deseamos es comparar entre dos aproximaciones a números de diferente magnitud. Dicho de otra forma, comparativamente, y teniendo en cuenta el tamaño de cada uno de los componentes de la pomada, qué error es mayor: ¿una diferencia de 0,00025 gramos respecto de 0,00285 ó de 0,00002 gramos respecto de 0,00015?
En el primer caso la proporción sería de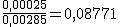 
, es decir de un 0,08 gramos por cada gramo de ácido bórico. Por tanto, de un 8%.
En el segundo componente la proporción sería de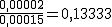 
, lo que implica una diferencia de 0,13 gramos por cada gramo de tetraborato. Un 13% de error.
Está claro que el error relativo del segundo componente es mayor, y en la mayoría de las ocasiones ese dato es el que importa.
Actividad
Se define error relativo de una aproximación a un número como el cociente entre el error absoluto y el valor del número. El error relativo se puede expresar en tanto por uno o en tanto por ciento.
En el ejemplo de la pomada, 0,087 es el error relativo del primer componente, y 0,133 es el error relativo del segundo.
AV - Reflexión
Objetivos
En el siguiente enlace a la página de Edad puedes repasar los conceptos que hemos desarrollado en este apartado.