5. Probabilidad
|
La probabilidad de un suceso es el valor alrededor del cual se
estabiliza un suceso que se realiza un número elevado de veces. La hoja
de cálculo nos permite hallar este valor sin necesidad de realizar el
suceso todas las veces.
En el siguiente ejercicio estudiaremos la probabilidad de obtener cada
uno de los seis números al tirar un dado. Guardaremos el libro con el
nombre "Probabilidad".
|
 |
|
Dados
Imagen de CEIP Els Cossetans |
Generar sucesos aleatorios
Para
estudiar la probabilidad de un suceso, éste se tiene que producir un
número elevado de veces. Evidentemente, no es necesario tirar los
dados muchas veces y apuntar el resultado de cada tirada. Para generar
los valores del experimento realizaremos un suceso aleatorio.
Actividad
La función matemática ALEATORIO genera números aleatorios entre 0 y 1.
En este caso, vamos a utilizar la función ALEATORIO anidada con la función ENTERO de la siguiente forma:
Recuerda que tienes que desactivar la función de cálculo automático en el menú "Herramientas" "Contenido de celdas". Después copia la función con el botón Autollenado y pulsa F9 para obtener los resultados aleatorios. Realiza la simulación de, al menos, 300 tiradas, ya que el objetivo es calcular la probabilidad del suceso en un número elevado de veces.
¡Ojo! Son números aleatorios y, por tanto, en tu ejercicio tendrás otros valores diferentes.
Cálculo de la probabilidad
Para calcular la probabilidad de que salga un número u otro,
necesitamos contar las veces que ha salido cada número en una cantidad
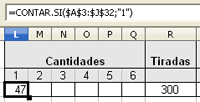
concreta de tiradas. Para ello vamos utilizar la función CONTAR.SI, cuyos argumentos son el rango y la condición que se debe cumplir.
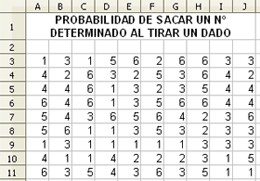
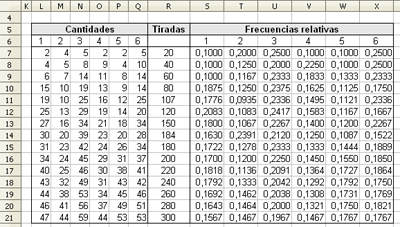
En este caso, hemos generado 300 tiradas que se muestran en el rango de celdas A3:J32. Si utilizásemos un número superior de sucesos, ampliaríamos este rango.
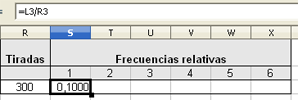
Para conocer la frecuencia relativa de cada suceso, calculamos el
número de veces que se repite el suceso entre el número total de
tiradas. A continuación puedes ver las fórmulas utilizadas para contar el número de sucesos y para calcular la frecuencia relativa de que salga el número 1 en 300 tiradas.
| Contar el nº de sucesos | Cálculo de la frecuencia relativa |
 |
 |
AV - Reflexión
Acabamos de calcular la cantidad y la frecuencia relativa de que salga el número 1 al tirar un dado. Completa la hoja de cálculo con el resto de sucesos y calcula las frecuencias relativas de que salgan los número 2, 3, 4, 5 y 6.
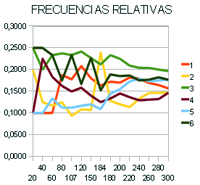Representación de las frecuencias
Para visualizar las frecuencias, se utilizan gráficos de línea donde cada frecuencia es una serie de datos en el eje Y y el número de lanzamientos son los datos de las categorías en el eje X.
Para que el gráfico se visualice correctamente, es necesario agrupar las tiradas por recuentos iguales, en este caso de 20 en 20 tiradas hasta llegar a completar las 300.
Los datos utilizados para crear el gráfico de frecuencias relativas son los siguientes:
Objetivos
Si observas la gráfica anterior, verás que al aumentar el número de tiradas, las líneas tienden a unirse en un punto.
Ahora puedes pasar un ratito jugando:
Si construyes la tabla de frecuencias podrás observar en el gráfico, como cuanto más repites el
experimento las frecuencias relativas se van aproximando a un valor.
Esta concidión se conoce como la Ley de los Grandes Números, según la cual la frecuencia relativa de los resultados de sucesos aleatorios, tiende a estabilizarse en un número denominado probabilidad del suceso.
En las siguientes páginas web encontrarás información sobre esta Ley y sobre el ejemplo más típico para entenderla que es la probabilidad de que salga cara o cruz al lanzar una moneda. Fíjate bien porque te servirá de ayuda para realizar la tarea.
AV - Pregunta de Elección Múltiple
Aunque hemos realizado un cálculo de
probabilidades, no podemos perder de vista que estamos trabajando con
una hoja de cálculo. Por tanto, las fórmulas utilizadas son las que
determinan los resultados.
Observa la tabla donde aparecen los conteos y las
frecuencias relativas para crear el gráfico y contesta a las siguientes
preguntas.
1) ¿Cuál es el rango utilizado para realizar el primer conteo de 20 tiradas?
|
a) A3:J3
| |
|
b) A3:J4
|
2) ¿Cuánto suman las cantidades de una fila (1,2,3,4,5,6)?
|
a) Siempre suman 20.
| |
|
b) La cantidad de las tiradas correspondientes.
|
3) Para hallar la frecuencia relativa de que salga el número 6 en 200 tiradas, ¿qué fórmula se utiliza?
|
a) Q16/R16
| |
|
b) SUMA(L16:Q16)
|
Pre-conocimiento
Un ejemplo de uso de la función ALEATORIO un poco más complejo es el que hemos encontrado en el siguiente blog. Se trata de construir un juego mediante OOo Calc en el cual se crearán el tablero, los dados, los marcadores de los jugadores y las preguntas:
Fuente: Youtube
Autor: cesarfractalis