2. Ámbito científico: Sistemas de numeración

Cuando contamos cantidades, hablamos de fechas o calculamos datos, utilizamos el sistema decimal. Es un sistema en base 10, es decir, utilizamos 10 dígitos para formar todos los números (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).

 

Cuando tratamos la información de forma digital, utilizamos otro sistema de numeración, el sistema binario. En este caso, la base es 2, es decir, utilizamos dos dígitos para formar los números (0, 1).

 

En el ámbito científico, también son importantes otros dos sistemas de numeración: el octal, sistema en base 8 (0, 1, 2, 3, 4, 5, 6, 7), y el hexadecimal, sistema en base 16 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).

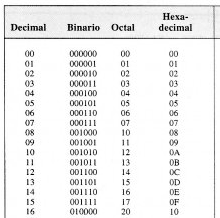
sistemas de numeración
 

Sistemas de numeración

Imagen de creación propia

 

 

Antes de comenzar a trabajar con la hoja de cálculo para realizar esta aplicación, es necesario tener en cuenta algunos aspectos: 

- En primer lugar, es necesario desactivar la opción de cálculo automático de OOo Calc, en el menú "Herramientas", "Contenido de celdas".

- A continuación, estableceremos el número máximo a convertir, en este caso será 255, que en sistema binario corresponde a 11111111 y, por tanto, estableceremos ocho columnas para colocar las ocho cifras que vamos a tener como máximo.

Icono de iDevice AV - Reflexión
Crea el libro "Sistemas de numeración" y da formato a la presentación de la hoja de cálculo que utilizaremos para convertir un número decimal a otros sistemas de numeración. Cambia el nombre de la hoja de cálculo denominándola "decimal".
Tanto las funciones que vamos a utilizar, como el análisis y tratamiento de los datos, constituyen la parte fundamental de la hoja de cálculo. Por tanto, la creación de las fórmulas es el paso determinante en cualquier aplicación de la hoja de cálculo.
 
En este caso, para realizar la conversión de un sistema de numeración a otro es necesario realizar tres pasos:
1. Multiplicar cada dígito del número original por la base elevada al peso correspondiente a su posición.
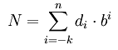
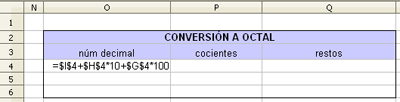
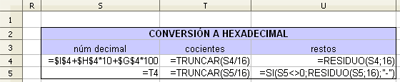
2. Realizar sucesivas divisiones por la base del sistema a convertir (entre 2 si es binario; entre 8 si es octal; entre 16 si es hexadecimal).
3. Determinar los restos de las divisiones, ya que éstos formarán las cifras del número en el sistema convertido, siendo el dígito de mayor peso el último cociente y el de menor peso el primer resto.
 

Conversión decimal-binario

Imágenes de creación propia

No estás en matemáticas y, por tanto, no es necesario que aprendas los fórmulas para convertir un sistema de numeración en otro. Esta explicación te servirá para comprender las funciones que vamos a utilizar para realizar la hoja de cálculo.

Icono IDevice Actividad

Las funciones utililizadas son:

 

- TRUNCAR: la función devuelve la parte entera del número, dividiéndolo entre la base.

- RESIDUO: la función devuelve el resto de la división del número entre la base.

- SI: la función condicional evalúa el resultado para pasar a la siguiente cifra.


Tutorial Función lógica SI
Y una vez aplicadas las funciones, el resultado es el siguiente:

 

conversión a binario

 

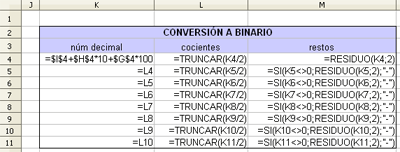
Recuerda que las celdas donde se ha introducido el número decimal son G4, H4, I4.

Icono de iDevice AV - Actividad de Espacios en Blanco
Ahora que ya has visto las fórmulas que tenemos que utilizar para convertir un número decimal a binario, seguro que eres capaz de escribir las fórmulas necesarias para convertirlo a octal.
 
 
Recuerda que el sistema octal es en base 8 y, por tanto, las divisiones se deben realizar entre 8.
 
conversión a octal
cocientes
 restos

  

Icono IDevice Objetivos
La conversión a hexadecimal es algo más complicada. Aunque el proceso es el mismo, hay que tener en cuenta que si el resultado de la función RESIDUO es mayor que 9, la cifra que debe aparecer es una letra.
 
conversión a hexadecimal

Esto supone que no podemos trasladar el número obtenido directamente de la conversión si no que es necesario utilizar otra fórmula. Se puede realizar una anidación de condicionales con la función SI o utilizar la función BUSCARV.
En este caso, hemos utilizado las función condicional anidada de la siguiente forma:
I7 → hexadecimal
H7 →
 hexadecimal

El resultado de la hoja de cálculo es el que aparece a continuación. Recuerda que cuando introduces un dato, para actualizar el resultado debes pulsar F9.
 
 
sistemas de numeración
Icono de iDevice AV - Actividad de Espacios en Blanco
Si has ido realizando la hoja de cálculo de la aplicación al ámbito científico sobre conversión de sistemas de numeración, te resultará sencillo comprobar el resultado de convertir los siguientes números decimales a sistema binario y a sistema octal.
Decimal
 10
 135 200
Binario
Octal
  

« Anterior | Siguiente »