1.3. Aplicando semejanza
Importante
En este curso vamos a estudiar la relación de semejanza que hay entre las rectas notables de un triángulo, considerando que el centro de dicha transformación siempre será uno de los vértices.
Mediana.
Como el vértice de semejanza se corresponde con la mediana conocida, la semejante tendrá la misma posición que la auxiliar.En la siguiente animación puedes ver cómo se construye un triángulo mediante semejanza, a partir de una mediana dada, recuerda que para construir el triángulo auxiliar debes de conocer al menos dos datos, por ejemplo, los ángulos Aº y Cº.
Bisectriz.
Como en el caso anterior, la bisectriz conocida tendrá la misma disposición que la auxiliar, por tanto, procederemos de la misma manera.
Observa en la siguiente animación que el centro de semejanza ahora es el vértice A, y los datos dados pueden ser dos de los ángulos.
Caso de estudio
 |
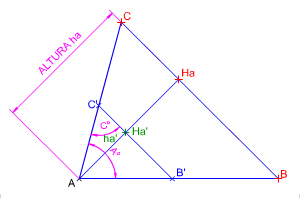En la imagen izquierda tienes la construcción de un triángulo escaleno conocida la posición de un vértice A, su ángulo Aº, su altura y el valor de otro ángulo Cº. En la resolución de este ejercicio hemos aplicado semejanza. |
| ¿Quieres ver cómo se ha resuelto? |