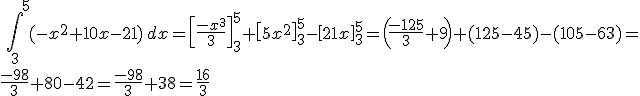3.2. Áreas Mágicas
Imagen de la Fundación Wikimedia bajo licencia Creative Commons.

Existen fenómenos que nos parecen inexplicables y que nos cuesta creer, pero, a pesar de los avances tecnológicos, encontramos situaciones que los científicos no pueden explicar. Casos como la construcción de las pirámides, los ovnis o la existencia del monstruo del lago Ness son cuestiones donde la comunidad científica discute sin llegar a un acuerdo unánime de su origen.

Entre muchos de estos misterios, vamos a destacar uno relacionado con lineas, "Las lineas de Nazca". Seguramente recordarás que trabajamos con ellas en la tarea del último tema de la Unidad 3. Estas lineas ubicadas en Perú, algunas con tamaños superiores a un kilómetro, fueron realizadas por la cultura nazca hace miles de años y el método para su construcción es un tema discutido por los científicos. Cabe destacar que su descubrimiento no se realizó hasta que el hombre pudo volar, ya que el gran tamaño de las figuras impide visualizarlas desde tierra.

Imágenes como un mono, una araña, un colibrí o un cóndor son las más famosas y conocidas, pero existen otras figuras con motivos geométricos menos espectaculares pero también muy meritorias.

La gran pregunta que se hacen los investigadores es cómo se pudieron construir estas grandes obras, con lineas perfectamente rectas en algunos casos, con medios tan rudimentarios. En este tema no vamos a analizar la longitud de las rectas pero sí el área que engloban algunas de las figuras de la cultura nazca.

 

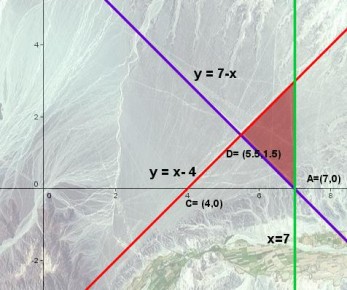
Observemos una de las figuras geométricas y calculemos el área de un triángulo que se aprecia perfectamente en la fotografía.

Imagenes tomada y transformada de la Fundación Wikimedia bajo licencia Creative Commons.

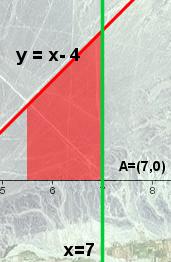
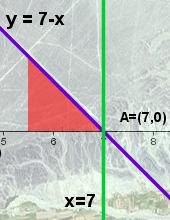
Para calcular el área deseada tan solo deberiamos determinar el área de la función y = x - 4 desde x = 5,5 hasta x = 7 y restarle el área de la función y = 7 - x también desde x= 5,5 hasta x = 7. En la imagen adjunta puedes apreciar las áreas indicadas.



Puedes observar que el primer área representa la expresión 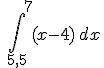con valor 3,375 y el segundo gracias a la integral 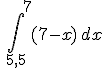con valor 1,125, por lo que el área deseada será 3,375-1,125 = 2,25 u2.

 

Pero ya sabemos que la resta de las integrales es la integral de la resta, por lo que podemos integrar la función obtenida de restar f(x) = x-4 y g(x) = 7-x.

r(x) = f(x) -g(x) = x -4 - (7-x)= 2x-11

 

Integrando la función 2x-11 entre 5,5 y 7, obtenemos el mismo resultado

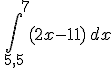= 2,25 u2.

 

 

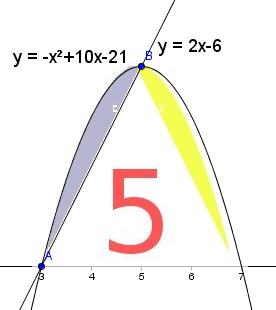Icono de iDevice Ejemplo o ejercicio resuelto

 

 

Debido a intereses económicos, algunas emisoras de televisión se han visto obligadas a unirse para poder sobrevivir. Como fusión de dos famosas emisoras, se obtiene el resultado de Antena 5. Para conservar el expíritu de ambas cadenas se ha decidido fusionar los logotipos de ambas, obteniendo el resultado que ves aqui.

 

El logotipo de la cadena de televisión Antena 5, está formado por figuras geométricas. La figura, tal y como puedes observar en el logotipo, está fomada por trozos de rectas y parábolas. Indica el área formada por la parte morada del logotipo.


Icono de IDevice de pregunta AV - Pregunta de Elección Múltiple
Imagen tomada y transformada del Banco de Imágenes del ITE.

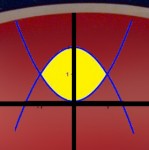
Una productora de zumos ecológicos ha decidido modificar la presentación de su envase de tetrabrik. El modelo elegido es el presentado en la imagen adjunta. Junto al diseño del envase, la compañía también ha cambiado el logo, formado por una combinación de figuras geométricas. La empresa fabricante de envases quiere realizar un encargo de tinta amarilla para imprimir el logo, pero necesita conocer cuantos cm2 necesita por cada envase.

Analizando el logo, aprecian que es el área formada por dos parábolas, la primera y = 2-x2 y la segunda y = x2 como puedes apreciar en esta otra figura.

Indica, con la ayuda de las indicaciones dadas, el área de la zona amarilla que aparece en el logo.


       
0

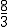
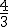
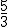
« Anterior | Siguiente »