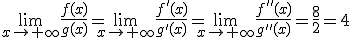3.1. ¡Ayuda con los límites!

|
| Foto tomada del Banco de Imágenes de Wikipedia. |
En multitud de ocasiones podemos realizar un mismo proceso de diversas formas y obtener el mismo resultado. Por ejemplo, para cocinar una receta de "Garbanzos con Bacalao", podemos cocinar los garbanzos de varias formas, con una olla express, cocinar los garbanzos en una cacerola a fuego lento, con uno de esos nuevos robots de cocinas, pero el resultado sigue siendo el mismo, un magnífico plato de garbanzos con bacalao.
Esto no ocurre solo en la cocina. Si me hace falta comprar un ordenador, puedo hacerlo en unos grandes almacenes, puedo adquirirlo por internet o llamando por teléfono a una tienda para que lo envíen por correo. El resultado es el mismo, disponer de un ordenador en casa para realizar este curso.
A la hora de calcular los límites, ocurre lo mismo, vamos a disponer de diversas herramientas para resolverlos. Algunos métodos nos gustarán más que otros, pero al igual que te ocurre como cuando cocinas los garbanzos con bacalao, si lo haces con la olla express, se cocinan más rápido, pero a fuego lento, salen más sabrosos.
Aquí vas a descubrir una nueva forma de calcular límites indeterminados, con la ayuda de la regla de L'Hôpital.
Si f y g son dos funciones derivables en el punto a verificando que 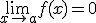 y
y 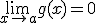 y además existe
y además existe 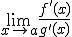 , podemos afirmar que
, podemos afirmar que
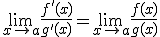
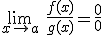 y
y 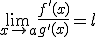 , entonces
, entonces 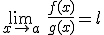
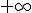 ó
ó 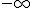 . Por otra parte, indicarte que también puedes utilizar la regla de L'Hopital para las indeterminaciones del tipo
. Por otra parte, indicarte que también puedes utilizar la regla de L'Hopital para las indeterminaciones del tipo 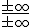 , es decir
, es decir
Si f y g son dos funciones derivables en el punto a verificando que 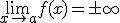 y
y 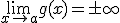 y además existe
y además existe 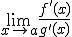 , podemos afirmar que
, podemos afirmar que
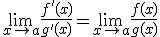
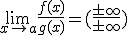 y
y 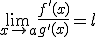 , entonces
, entonces 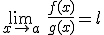
Determina el siguiente límite 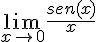
Determina el siguiente límite: 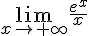
|
0
| |
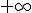
| |
|
| |
|
1
|
 |
|
Foto del Banco de imágenes de Wikipedia. |
En un lago situado en la sierra vive una población de carpas que, en ausencia de predadores, seguiría una función de crecimiento 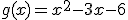 , donde x indica el número de años que transcurre desde que se inserta la carpa en el ecosistema y f(x) simboliza el número de carpas que hay en el estanque transcurridos x años.
, donde x indica el número de años que transcurre desde que se inserta la carpa en el ecosistema y f(x) simboliza el número de carpas que hay en el estanque transcurridos x años.
Por otro lado, las carpas se alimentan, entre otras cosas, de un tipo especial de plantas que sigue una función de crecimiento 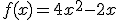 donde x indica también el número de años transcurridos y g(x) el peso (en kilos) que alcanza la colonia de plantas después de x años. Si el número de plantas que come cada carpa viene expresada por la función
donde x indica también el número de años transcurridos y g(x) el peso (en kilos) que alcanza la colonia de plantas después de x años. Si el número de plantas que come cada carpa viene expresada por la función 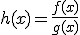 , indica la cantidad de plantas (en kilos) que puede ingerir cada carpa cuando el número de años se haga muy grande.
, indica la cantidad de plantas (en kilos) que puede ingerir cada carpa cuando el número de años se haga muy grande.
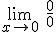 .
.
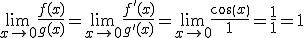
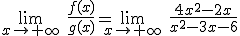 . Observamos que es una indeterminación del tipo
. Observamos que es una indeterminación del tipo 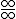 .
.
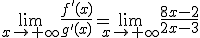 .
.
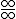 , pero podemos volver a derivar de nuevo.
, pero podemos volver a derivar de nuevo.