2.1. Construyendo funciones
 |
| Imagen tomada del Banco de Imágenes de wikipedia |
En este tema pretendemos obtener el resultado óptimo en diversas situaciones, pero la pregunta que nos acecha es: ¿Qué optimizo? ¿Una situación? ¿Cómo es eso?¿Cuáles son los instrumentos que poseemos para poder buscar esa solución máxima?
Convertir la realidad que nos rodea en funciones no es tarea fácil ya que, en ocasiones, no es trivial identificar algunas funciones conocidas con la situación planteada y además pueden influir más de una variable.
En este apartado vamos a dar algunas pautas para fabricar las funciones y te irás familiarizando con la "construcción" de las funciones necesarias.
Para construir nuestra función, debemos tener claro la función a optimizar, ya sea área, volúmenes, costes...en la que intervendrán dos variables. Por otro lado, debemos buscar una condición que relacione ambas variables, donde despejaremos una y la sustituiremos en la función a optimizar, de tal forma que nuestra función se convierta en una función de una sola variable, en lugar de dos.
Para construir una función con objeto de optimizarla debemos:
1. Representar gráficamente el problema, si es posible.
2. Identificar las variables que intervienen en la función :"Llamamos x la variable tal, e y a la variable cual"
3. Preguntarnos cual es la función a optimizar , la función a la que queremos calcular máximos o mínimos . Debes tener en cuenta que puede tener una o dos variables. Estas funciones suelen estar relacionadas con áreas, volúmenes, costes...
4. Relacionar las variables, x e y, de la función a optimizar, mediante una condición que exista entre ambas.
5. Despejar una de las variables de la condición y sustituir en la función a optimizar.
Así obtenemos una función, de una variable, con la que trabajaremos en el siguiente apartado.

 Ángela tiene un pequeño terreno en las afueras de su localidad. Un vecino le ha regalado un trozo de tela metálica de 10 metros de largo y ella pretende aprovecharla para la construcción de una valla para un jardín, ya que las gallinas picotean las flores.
Ángela tiene un pequeño terreno en las afueras de su localidad. Un vecino le ha regalado un trozo de tela metálica de 10 metros de largo y ella pretende aprovecharla para la construcción de una valla para un jardín, ya que las gallinas picotean las flores.
El jardín tendrá forma triangular, de tal forma que una pared, formará la hipotenusa y la tela metálica los catetos.
¿Cual será la función, de una sola variable, que nos indique el área del jardin propuesto?
Utiliza el punto para indicar los decimales.
La función buscada es ·x - x2

Un conocido operador de cable, "Golazos TV" tiene actualmente 500000 abonados, que abonan mensualmente 30 €. Tras un estudio de mercado, los gestores llegan a la conclusión que por cada euro rebajado, el número de abonados aumentarían en 20000 ¿Cuál es la función que proporciona el beneficio de la operadora en función de los nuevos abonados?
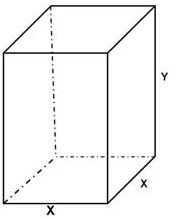 Estudiemos en primer lugar la función solicitada. La cantidad de chapa utilizada será el área de un prisma de base cuadrada. Llamaremos x al lado de la base cuadrada e y a la altura del prisma.
Estudiemos en primer lugar la función solicitada. La cantidad de chapa utilizada será el área de un prisma de base cuadrada. Llamaremos x al lado de la base cuadrada e y a la altura del prisma.
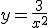 . Sustityendo en la función, obtenemos
. Sustityendo en la función, obtenemos