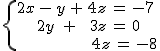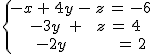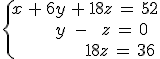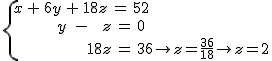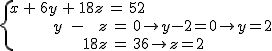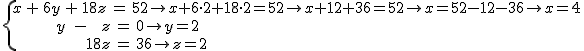3.1. Todo consiste en reducir
Ejemplo o ejercicio resuelto
Vamos a replantear el problema con el que empezamos el tema.
 |
| 5. Imagen de opendeco.es bajo licencia Creative Commons |
Si recuerdas, estando Ana en la tienda de Juan, observa que una persona se lleva calcetines, camisetas y camisas y paga 52 €. Antes había visto que los pares de calcetines estaban a 1 €, las camisetas a 6 € y las camisas a 18 €. Y como quería saber el número de prendas de cada tipo que compraba el caballero, había llamado x= nº calcetines; y= nº camisetas; z= nº camisas.
Ahora vamos a añadir dos nuevas restricciones, y es que, sabemos que el caballero compró tantas camisetas como camisas y que en camisas se gastó 36 €.
¿Cuántos calcetines, camisetas y camisas compró el caballero?
Como hemos visto en el ejemplo, si tenemos un sistema en el que en cada ecuación hay una incógnita menos, encontrar la solución es muy fácil, pues basta calcular el valor de la incógnita de la última ecuación e ir sustituyendo en las anteriores.
Actividad
La clave estará en reducir el sistema que nos den a uno del tipo anterior, es decir, a un sistema que tenga:
 |
Una ecuación con tres incógnitas, otra con dos incógnitas y una última con una sola incógnita.
Cuando el sistema está de esa forma decimos que está escalonado o en forma escalonada.
Para conseguir que el sistema sea escalonado utilizaremos procedimientos similares a los usados en el método de reducción.
AV - Reflexión
Vamos a practicar antes de seguir.
Resuelve los sistemas:
