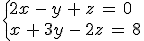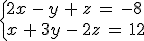2. Sistemas con varias ecuaciones

En numerosas ocasiones se nos presentan situaciones en las que tenemos que poner varias incógnitas, como hemos visto anteriormente, y en las que tenemos que imponer varias restricciones por la propia información que disponemos.

Perchero de una tienda de ropa
3. Imagen de ex novo bajo licencia Creative Commons.

 

Por ejemplo, imagínate que en la situación anterior, Ana sabe también que en total el caballero ha comprado 8 artículos.

Ahora además de saber que se ha gastado 52 euros, sabemos que ha comprado sólamente 8 artículos, así que por ejemplo la solución, 4 pares de calcetines, 5 camisetas y 1 camisa ya no nos vale.

Ahora podríamos plantear una nueva ecuación que relacione las incógnitas con ese nuevo dato. Puesto que x, y, z medían el número de calcetines, de camisetas y de camisas respectivamente, tendríamos que:

x + y + z = 8.

 

Uniendo las dos ecuaciones tendríamos que cualquier solución del problema deberá satisfacer ambas:

 

Esto da lugar a un sistema de ecuaciones.

 

Icono IDevice Actividad
Como hemos visto en el tema anterior, un sistema de ecuaciones lineales es un conjunto de dos o más ecuaciones lineales con varias incógnitas para el que se quiere encontrar una solución común, es decir, una solución del sistema debe ser un conjunto de valores, uno para cada incógnita, que cumpla TODAS las ecuaciones.

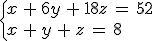
El sistema anterior con dos ecuaciones y tres incógnitas sigue teniendo muchas soluciones, menos que al principio, pero sigue siendo infinito el número de soluciones, teniendo en cuenta números decimales y negativos.

 

Por ejemplo, puedes comprobar que: x=-0,8, y= 8,8, z= 0 es una solución del sistema anterior.

 

Otra podría ser x=1,6 y=5,4 z=1, y así hasta infinitas posibilidades.

Icono IDevice Actividad

Para que un sistema de ecuaciones tenga una única solución deberemos tener al menos tantas ecuaciones como incógnitas.

Camiseta del Betis con el 3 a la espalda

Por tanto si planteamos problemas con tres incógnitas, deberemos obtener tres ecuaciones para encontrar su única solución.


AV - Pregunta Verdadero-Falso

Contesta verdadero o falso a las siguientes cuestiones:

 


 



1) x=1, y=3, z=1 es una solución del sistema:

 


 

 


Verdadero Falso     


2) El sistema anterior tiene una única solución.

Verdadero Falso


3) El trío x=0, y=4, z=-4 es solución del sistema:

 

 


Verdadero Falso
AV - Pregunta de Selección Múltiple

Señala los tríos que sean solución del sistema:

 


 

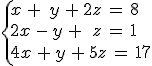
(-1, 1, 4)
(3, 5, 0)
(4, 2, 1)
( 1.5 , 3.5 , 1.5)



« Anterior | Siguiente »