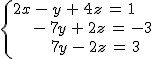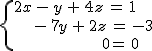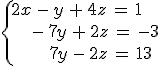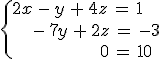4. A veces muchas, a veces ninguna
Todos los sistemas del punto anterior podían resolverse y encontrábamos una solución para cada incógnita. Es decir, el sistema tiene una única solución.
Como ya vimos en el tema anterior, cuando ocurre esto, decimos que el sistema es COMPATIBLE DETERMINADO.
|
Hay veces en las que a pesar de tener tres ecuaciones en el sistema, una de ellas no aporta ninguna información nueva; no añade nada nuevo, por lo que en realidad tenemos dos ecuaciones y por tanto infinitas soluciones para el sistema.
Esto ocurre cuando al aplicar el método de Gauss en el último paso, sucede que se van todas las incógnitas y los términos independientes, es decir, llegamos al caso en el que la última ecuación queda:
0=0
Como esto siempre es verdad, volvemos a insistir en que el sistema tendrá infinitas soluciones.
En este caso, como vimos en el tema anterior, decimos que el sistema es COMPATIBLE INDETERMINADO.
Actividad
Un sistema de ecuaciones diremos que es compatible indeterminado si tiene infinitas soluciones.
Esto ocurre si al resolver el sistema, llegamos a la situación 0 = 0 y nos quedamos con menos ecuaciones que incógnitas.
Ejemplo o ejercicio resuelto
Vamos a resolver el siguiente sistema y vamos a ver que ocurre lo que acabamos de comentar:
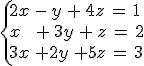
Igualmente puede ocurrir que al aplicar el método de Gauss, la parte de las incógnitas desaparezca en la última ecuación, pero no así los términos independientes.
En este caso llegamos a una situación de la forma:
 |
| 11. Foto de Humboldthead con licencia Creative Commons |
0 = K, con K un número distinto de cero.
Como eso no es verdad, llegamos a que el sistema no tiene solución. A estos sistemas, como ya vimos, se les llama SISTEMAS INCOMPATIBLES.
Actividad
Un sistema de ecuaciones decimos que es incompatible si carece de solución.
Esto ocurre cuando al aplicar el método de Gauss, llegamos a la situación 0 = k, y por tanto, en una ecuación se van las incógnitas pero no los términos independientes.
Ejemplo o ejercicio resuelto
Vamos a ver que el siguiente sistema no tiene solución:
AV - Pregunta de Elección Múltiple1.- El sistema de ecuaciones
|
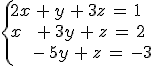
Es Compatible Determinado
| |
|
Es Compatible Indeterminado
| |
|
Es un sistema incompatible
|
2.- El sistema de ecuaciones:
|
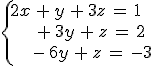
Es un sistema Compatible Determinado
| |
|
Es un sistema Compatible Indeterminado
| |
|
Es indeterminado
|