1. Tres incógnitas, una ecuación
Ejemplo o ejercicio resuelto
El otro día estaba mi hermana Ana en la tienda de Juan y mientras observaba la ropa
 |
| 2. Imagen de blog.jmc.bz bajo licencia Creative Commons |
de los estantes, escuchó la conversación entre Juan y un caballero.
Juan: Bien pues entonces lleva usted calcetines, las camisetas y estas camisas.
Caballero: Sí, exacto.
Juan: Muy bien, pues son 52 euros.
Ana vió los precios de las ofertas y éstos marcaban: "calcetines: 1 €", "camisetas 6 €" y "camisas 18 €"
Entonces se preguntó, ¿cuánto habrá comprado de cada cosa?
Actividad
Una ecuación lineal con tres incógnitas es una ecuación de la forma:
a·x + b·y + c·z = d
Una solución de esta ecuación es un trío de valores; uno para x, otro para y y otro para z.
Cualquier ecuación con tres incógnitas tiene infinitas soluciones, pues basta darle un valor cualquiera a una incógnita (por ejemplo, "x"), otro valor a otra (por ejemplo, "y") y ajustar el valor que tiene que tener la tercera(sería en nuestro caso "z") para que se cumpla la igualdad.
AV - Pregunta Verdadero-FalsoVerdadero Falso
Verdadero Falso
Verdadero Falso
Verdadero Falso
Si recuerdas, en el tema anterior, cuando queríamos encontrar soluciones de una ecuación con dos incógnitas, le dábamos valores a una de ellas y cálculabamos el valor que le correspondía a la otra haciendo que se cumpliera la ecuación.
Bien, pues ahora, como hemos comentado arriba, al tener tres incógnitas, tendremos que darle valores a dos de las incógnitas y calcular el que le corresponde a la tercera sustituyendo en la ecuación y despejando.
Por ejemplo, si tenemos la ecuación:
x + 2y - 3z =4
y queremos calcular una solución, le damos por ejemplo, el valor 1 a la "y" y el 0 a la "z".
Así nos quedaría:
x + 2·1 - 3·0 = 4
de donde
x + 2 = 4
y por tanto x = 2, luego una solución sería: x = 2; y = 1; z = 0.
Si quisiéramos otra solución, bastaría con darle otros dos valores a dos letras y volver a sustituir y despejar. Por ejemplo, podemos ahora hacer que x valga 1 e y valga 0. Entonces:
1 + 2·0 - 3z = 4
de donde
1 - 3z = 4
y despejando, z = 3/(-3); o sea z = -1.
Luego otra solución sería: x = 1; y = 0; z = -1
Y así podríamos seguir de manera infinita, por tanto, existen infinitas soluciones, infinitos tríos para esta ecuación.
Objetivos
Al igual que las soluciones de una ecuación con dos incógnitas se representaba como una recta en el plano, podemos representar gráficamente las infinitas soluciones de una ecuación con tres incógnitas.
En este caso, el significado geométrico es un plano en el espacio. Es decir, todas las soluciones de una ecuación lineal con tres incógnitas se representan gráficamente como un plano.
 |
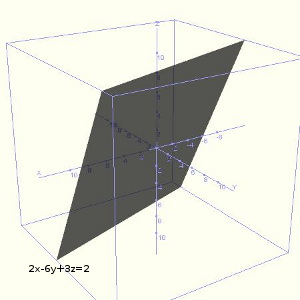Por ejemplo, la imagen de la derecha muestra la gráfica del plano:
2x - 6y + 3z = 2,
en el espacio.
Los puntos sombreados serían todos los puntos que son solución de la ecuación.
Para obtenerlo con WIRIS debes usar la función dibujar3d:
