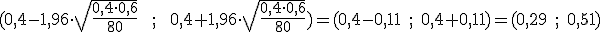2.1. Tratamiento médico
 |
| Imagen de universidadcatolica bajo licencia Creative Commons |
¿Qué tal vamos? ¿Qué te parece esto de los intervalos de confianza? ¿Sabías que estos estudios se utilizan mucho en los laboratorios farmacéuticos para comprobar tratamientos médicos?
Como ya te habrás dado cuenta, el hecho de calcular intervalos de confianza, es una técnica que nos permite hacer afirmaciones sobre qué valores podemos esperar para un parámetro, en este caso para la proporción.
Este intervalo que calculamos depende de varios factores:
- Del parámetro que estimemos en la muestra (proporción media, etc.)
- Del tamaño de la muestra. Cuanto mayor sea el tamaño muestral, menor será la diferencia entre el valor estimado y el valor real desconocido.
- De la probabilidad con la que el método dará una respuesta correcta, es decir, el nivel de confianza. Los niveles de confianza habituales son el 95% y el 99%.
Actividad
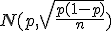, donde p es el parámetro poblacional que se quiere estimar, aproximando su valor mediante el valor del estadístico 
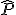obtenido de la muestra.
Ejemplo o ejercicio resuelto
|
| Imagen de ruurmo bajo licencia Creative Commons |
Nuestra empresa farmacéutica quiere probar una nueva vacuna destinada a jóvenes de entre 12 y 18 años. Para ello, piensan hacer una prueba y aunque creen que los efectos secundarios (dolor de cabeza, vómitos, etc.) son mínimos, antes de sacarla al mercado encargan a Tisbet Survey que seleccione una muestra y aplique el tratamiento.
La muestra está formada por 500 jóvenes, produciendo efectos secundarios en el 5 % de ellos.
.
.
Actividad
El intervalo de confianza para la proporción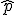 
es:
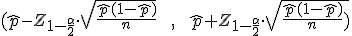
donde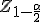 
es el valor crítico para el coeficiente de confianza 
.
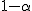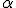es el nivel de significación o de riesgo.
El margen de error es la diferencia entre los extremos superior e inferior del intervalo de confianza.
AV - Pregunta de Elección Múltiple |
|
Imagen de the italian voice bajo licencia Creative Commons |
La empresa farmacéutica elabora una revista mensual donde informa de nuevos avances médicos y la reparte por los centros educativos del pueblo.
En el IES "Benito V." se ha tomado una muestra de 80 alumnos y ha dado como resultado que 32 alumnos leen la revista.
a) Calcula la proporción muestral de lectores de la revista.
|
0,2
| |
|
0,4
| |
|
0,8
|
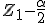es:
|
0,68
| |
|
1,96
| |
|
2,58
|
|
Verdadero. | |
|
Falso
|
|
2 %
| |
|
22 %
| |
|
29 %
|
En esta escena de GeoGebra creada por José Álvarez y modificada por José María Vázquez de la Torre, puedes ver cómo son los intervalos de confianza para la proporción.
Pre-conocimiento
Usando el mundial de fútbol para aprender intervalos de confianza.
En la página que te mostramos a continuación te demuestro como ser mejor que Cristiano Ronaldo lanzando penaltis usando intervalos de confianza.
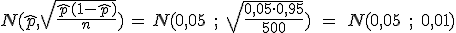
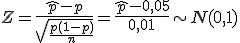
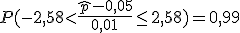