2.1. La Desviación
 |
| Imagen de Habladorcito con licencia Creative Commons |
Vamos a calcular cuanto se desvían de la media los datos del grupo de 2ºA. Veamos de nuevo las calificaciones de nuestros dos grupos de alumnos:
| 2º Bachillerato A | |
| Calificaciones | N.º de Alumnos |
| [0,2) | 7 |
| [2,4) | 6 |
| [4,6) | 4 |
| [6,8) | 6 |
| [8,10] | 7 |
Lo primero que haremos será calcular su media:
| Calificaciones | Marcas de clase(xi) |
Nº de alumnos(fi) |
xi·fi |
| [0,2) | 1 |
7 |
7 |
| [2,4) |
3 | 6 | 18 |
| [4,6) |
5 | 4 | 20 |
| [6,8) |
7 | 6 | 42 |
| [8,10] |
9 | 7 | 63 |
| N=30 | Suma =150 |
La media será: 
Una vez que tenemos el valor de la media calcularemos la diferencia de cada elemento con respecto a este valor y calcularemos la media aritmética de estas diferencias. Nos ayudaremos de una tabla similar a la anterior donde añadiremos la columna 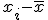 .
.
| Calificaciones | xi |
fi |
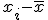 |
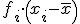 |
| [0,2) | 1 |
7 |
1-5=-4 | -28 |
| [2,4) |
3 | 6 | 3-5=-2 | -12 |
| [4,6) |
5 | 4 | 0 | 0 |
| [6,8) |
7 | 6 | 2 | 12 |
| [8,10] |
9 | 7 | 4 | 28 |
| N=30 | Suma=0 |
Puedes observar que se compensan las sumas positivas con las negativas. Esto va a suceder siempre así y nos indicaría que a desviación siempre sería cero, cosa que no es cierta. Para resolver esta situación elevaremos al cuadrado esta diferencia. En matemáticas realizar esta operación tiene que ver con el cálculo de la distancia a un punto, y esto tiene cierta lógica, pues estamos calculando la distancia de los datos a la media. Ahora ya no se compensan los positivos con los negativos, ya que todos los valores serán positivos y, por lo tanto, ya no se anularán al sumarlos. Veamos como quedaría la tabla:
| Calificaciones | xi |
fi |
 |
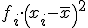 |
| [0,2) | 1 |
7 |
16 |
112 |
| [2,4) |
3 | 6 | 4 | 28 |
| [4,6) |
5 | 4 | 0 | 0 |
| [6,8) |
7 | 6 | 4 | 28 |
| [8,10] |
9 | 7 | 16 | 112 |
| N=30 | Suma=280 |
La desviación será la media aritmética de todas las diferencias y vendrá dada por la suma de todos los 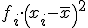 , celda de color verde, dividida por el número total de elementos (N=30).
, celda de color verde, dividida por el número total de elementos (N=30).
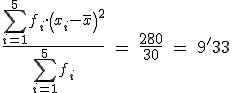
La varianza de una distribución estadística es la media aritmética de los cuadrados de las desviaciones respecto de la media. Se repreesenta por s2. (Recuerda que si la varianza es referida a una población en vez de a una muestra se representa por σ2 )

Cuanto más pequeña sea la varianza de una distribución mayor es el grado de representatividad de la media.
 |
| Imagen de edans con Licencia Creative Commons |
| 2º Bachillerato B | |
| Calificaciones | Nº de Alumnos |
| [0,2) | 2 |
| [2,4) | 7 |
| [4,6) | 12 |
| [6,8) | 7 |
| [8,10] | 2 |
¿En cuál de los dos cursos la media es más representiva?
Un inconveniente de la varianza es que no tiene las mismas unidades que los datos. Si estamos midiendo, por ejemplo, el número de hijos en familias de un determinado lugar, la varianza nos dará el resultado en número de hijos al cuadrado, mientras que su raíz cuadrada vendrá medida en número de hijos. Por ello se usa la raíz cuadrada de ese parámetro. Este nuevo valor tiene las mismas unidades que los datos, lo que facilita su interpretación y le da un sentido.
Se llama desviación típica de una variable estadística a la raíz cuadrada positiva de la varianza y se representa por s (recuerda que la desviación típica referida a una población se representa por σ).
La desviación típica es el medidor de la dispersión más usado en Estadística Descriptiva. Al igual que ocurre con la varianza, cuanto menor sea este valor más representativa será la media.
En la siguiente tabla se muestran los resultados del estudio sobre el peso en alumnos de 2º de Bachillerato que se está llevando a cabo en nuestro centro "Benito V."
| Peso en Kg. |
[50,56) | [56,62) |
[62,68) |
[68,74) |
[74,80) |
[80,86] |
| Nº de Alumnos |
12 | 25 | 25 |
20 |
12 |
6 |
Calcula la media, la varianza y la desviación típica de la distribución.
Los ordenadores nos permiten calcular de forma más rápida las tablas de frecuencia que usamos habitualmente en este tema. Las hojas de cálculo van a ser las encargadas de realizar este trabajo. En este vídeo elaborado por Laureano Serrano te mostramos como calcular la media y la desviación típica con ayuda del programa Calc de OpenOffice.
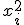 y
y 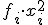 ya que vamos a aplicar la segunda parte de la fórmula de la varianza:
ya que vamos a aplicar la segunda parte de la fórmula de la varianza:
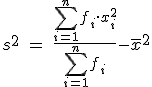

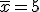 .
.