1.4. ¡A lo mejor nos interesa agrupar!
 |
| Imagen de amiramora bajo licencia Creative Commons |
El equipo de baloncesto de la ciudad le ha encargado a TisBet Survey que haga un estudio de la altura de todos los alumnos y alumnas de Secundaria.
En lugar de hacer un muestreo de todos los chicos y chicas de la ciudad, la empresa se plantea elegir algunos barrios, ya que con respecto a la altura, los barrios son como ”pequeñas poblaciones” comparables a la ciudad.
En este caso ¿podemos simplificar la elección de la muestra al elegir los barrios sin perder precisión?
La respuesta es que en este caso, podríamos elegir barrios y analizar las alturas de los estudiantes de cada barrio sin perder precisión.
El método que nos permite hacer esto es el muestreo por conglomerados.
La población se divide en unidades o grupos, llamados conglomerados (generalmente son unidades o áreas en los que se ha dividido la población), que deben ser lo más representativas posible de la población, es decir, deben representar la heterogeneidad de la población objeto del estudio y ser entre sí homogéneos.
El motivo para realizar este muestreo es que a veces resultaría demasiado costoso realizar una lista completa de todos los individuos de la población objeto del estudio, o que cuando se terminase de realizar la lista no tendría sentido la realización del estudio.
El principal inconveniente que tiene es que si los conglomerados no son homogéneos entre sí, la muestra final puede no ser representativa de la población.
Decimos que un muestreo es aleatorio por conglomerados cuando dividimos la población en conjuntos o conglomerados.
Se eligen al azar unos pocos de estos conglomerados y la muestra estará formada por todos los elementos de ellos o por muestras aleatorias simples de éstos.
 |
|
Imagen de microlito bajo licencia Creative Commons |
A la empresa TisBet Survey le han encargado que haga un estudio sobre el estado de los libros de todas las bibliotecas municipales de la ciudad.
¿Qué tipo de muestreo deben utilizar?
Verdadero Falso
Verdadero Falso
 |
| Imagen de joaoa bajo licencia Creative Commons |
Volvamos al ejemplo del instituto "Benito V.".
Recuerda que queríamos tomar una muestra de 28 alumnos de los 560 que hay en el centro educativo y que el factor de elevación era de 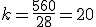 .
.
Numeramos a los alumnos del 1 al 560. Elegimos entonces un número x al azar entre 1 y 20 y ese será el primer alumno seleccionado, el que ocupa el lugar x.
Luego tomamos el x+20, x+2·20 y así sucesivamente.
Este tipo de muestreo se le llama sistemático y no es aleatorio porque todas las muestras no son igualmente probables.
- El muestreo sistemático es equivalente al muestreo aleatorio si los elementos se encuentran numerados de manera aleatoria.
- El muestreo sistemático puede considerarse un caso particular del muestreo por conglomerados, estando cada uno de ellos formado por los siguientes elementos que ocupan en la lista el lugar:
Primer conglomerado: 1, 1 + k, 1 + 2·k, 1 + 3·k, 1 + 4·k, . . .
Segundo conglomerado: 2, 2 + k, 2 + 2·k, 2 + 3·k, 2 + 4·k, . . .
. . .
k-ésimo conglomerado: 20, 2·k, 3·k, 4·k, . . . n·k.
Seleccionar una muestra sistemática equivale a seleccionar al azar un único conglomerado. Para ello es necesario que cada uno de los conglomerados definidos tenga una composición similar a la población.
- También puede considerarse como un caso particular de muestreo estratificado con un número de estratos igual a n, cada uno de ellos con k elementos de manera que en cada estrato se elige un único elemento.
En el muestreo estratificado el elemento seleccionado en cada estrato es aleatorio, mientras que en el sistemático se elige de forma aleatoria al primer elemento quedando los restantes determinados por el factor de elevación k.
Decimos que un muestreo es aleatorio sistemático cuando seleccionamos los n elementos de la muestra de k en k siendo k el factor de elevación:
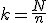
N es el número de elementos de la población y n el tamaño de la muestra.

|
|
Imagen de palm_z bajo licencia Creative Commons |
Este año la vuelta ciclista a España tiene la meta en la ciudad donde está la oficina de TisBet Survey y además la organización quiere realizar un control antidopaje y han pedido ayuda a esta empresa para ver cómo deberían seleccionar a los ciclistas.
¿Cómo crees que deberían hacerlo?