1.3. Siempre hubo clases
 |
| Imagen de Miguel Vera bajo licencia Creative Commons |
A veces puede interesarnos hacer otro tipo de muestreo que no sea el aleatorio simple.
Imagina que queremos hacer un estudio para saber a qué dedican su tiempo libre las personas que viven en tu ciudad. Todos sabemos que los ancianos no realizan el mismo tipo de actividades que los jóvenes, ni tampoco que las personas de mediana edad, como por ejemplo tus padres. Nos interesaría entonces que toda esta información que tenemos de antemano nos ayude a construir una muestra más significativa. De hecho, nos interesa que todos esos colectivos estén representados en nuestra muestra.
A los colectivos que hemos definido, en este caso por edad, los llamaremos estratos. Lo que haremos será dividir nuestra muestra de manera que haya representantes de todos los estratos.
A este tipo de muestreo lo llamamos muestreo estratificado.
Decimos que un muestreo es aleatorio estratificado cuando dividimos la población en subgrupos o estratos homogéneos y en cada uno de ellos tomamos muestras aleatorias simples.
Para hacer los subgrupos, seguiremos el criterio de formarlos de tal manera que haya la máxima homogeneidad en relación con la variable a estudio dentro de cada estrato y la máxima heterogeneidad entre los estratos.
Respecto al reparto del tamaño de la muestra en los diferentes estratos o subpoblaciones, consideraremos distintos criterios de afijación: afijación igual si todos los estratos tienen el mismo número de elementos en la muestra y afijación proporcional si cada estrato tiene un número de elementos en la muestra proporcional a su tamaño.

|
|
Imagen de IES Bajo Guadalquivir bajo licencia Creative Commons |
En el instituto "Benito V." se quiere pasar una encuesta tomando una muestra de 28 alumnos considerando el curso al que pertenecen.
El número de alumnos por niveles es el siguiente:
| Curso | Nº de alumnos/as |
| 1º ESO |
120 |
| 2º ESO |
120 |
| 3º ESO |
100 |
| 4º ESO |
90 |
| 1º Bach. |
70 |
| 2º Bach. |
60 |
a) ¿Qué tipo de muestreo tendríamos que utilizar?
b) ¿Cómo sería la muestra si hacemos la encuesta solamente en el primer ciclo de Secundaria?
c) Siguiendo el criterio del curso y considerando todo el centro educativo, ¿cómo sería la muestra?
Con la siguiente escena de Descartes de María Vicenta Cabalgante Perera, puedes calcular el número de elementos de cada estrato en la muestra.
En el caso de afijación igual, elegimos el mismo número de alumnos de cada estrato dividiendo el número de elementos que queremos en la muestra entre el número de estratos.
En la escena de Descartes para obtener el número de elementos en cada estrato basta con introducir el número de estratos y el tamaño de la muestra.
En el caso de afijación proporcional, para cada estrato hay que hacer una proporción, por tanto, basta con dividir el tamaño de la muestra entre el tamaño de la población y multiplicar por el tamaño de cada estrato. En la escena basta con introducir el tamaño de la población, el tamaño de la muestra y el tamaño de un estrato y obtendremos los elementos de la muestra que debemos elegir en ese estrato.
En el barrio donde se encuentra la oficina de TisBet Survey, viven unos 1500 niños y jóvenes, 7500 adultos y 1000 ancianos.
El ayuntamiento de la localidad se está planteando la construcción de un parque de atracciones, para lo cual decide encargarle a TisBet Survey que haga una encuesta sobre los gustos de ocio y aventura a una muestra de 200 individuos elegidos al azar.
Para ello se utiliza un muestreo estratificado.
¿Cuál será el tamaño muestral correspondiente a cada estrato?
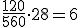 alumnos.
alumnos.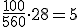 alumnos.
alumnos.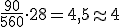 alumnos.
alumnos.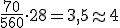 alumnos.
alumnos.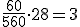 alumnos.
alumnos.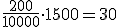 .
.
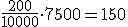 .
.
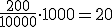 .
.