A nuestra empresa TRANS VELOX nos ha llegado la oferta del transporte de pescado a las ciudades de Córdoba, Granada y Sevilla. El origen de la mercancía procede de las ciudades de Málaga y Cádiz.

En la siguiente tabla puedes ver los costes, en euros, de transportar una caja de pescado desde las ciudades costeras a las ciudades interiores:

	Córdoba	Granada	Sevilla
Cádiz	2	3	1
Málaga	1	1	2

La oferta desde la ciudad de Málaga es de 250 cajas, y desde Cádiz es de 150. La demanda desde Sevilla es de 200 cajas, 150 por parte de Córdoba y 50 por parte de Granada.

¿Cuál es la mejor opción para distribuir el pescado de forma que los costes de transporte sean los más bajos posibles y de forma que todas las ciudades de destino sean totalmente abastecidas con las cantidades demandadas?

1. Organizamos los datos

Lo primero que hacemos, como siempre es organizar los datos en una tabla. Haz clic sobre la presentación para ver la construcción de la tabla.

La función objetivo será el total del número de cajas enviada entre dos ciudades multiplicado por lo que cuesta cada envío:

2x+1(150-x)+3y+1(50-y)+1(150-x-y)+2(x+y+50)=2x+3y+450

Min F(x,y)=2x+3y+450

Las restricciones del problema salen de obligar a que todas las variables de a tabla anterior sean positivas o nulas.

Por lo tanto, se debe resolver el siguiente problema de programación lineal:

 

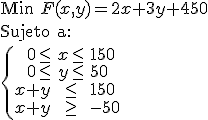
2. Resolvemos el problema

Como puedes ver en la escena siguiente de Geogebra el valor mínimo de nuestra función objetivo se alcanza en el punto A(0,0) y toma un valor de 450. Puedes mover el deslizador k y ver como va variando el valor de la función objetivo

La restricción x+y>-50 es redundante, es decir, no es necesaria; pues, aunque no la incluyamos, la región factible sigue siendo la misma.

3. Conclusión

La solución a nuestro problema, x=0 e y=0, consiste en enviar 150 cajas a Córdoba desde Málaga, 50 cajas a Granada desde Málaga, 150 cajas a Sevilla desde Cádiz y 50 cajas a Sevilla desde Málaga.