2.2. Comida para perros
 |
| Imagen de Natalia Lobato bajo licencia Creative Commons |
La empresa "Mi Mascota, S.A." se dedica a la elaboración de comida para mascotas. Están trabajando en la elaboración de un nuevo producto para la alimentación de perros teniendo en cuenta que tiene que cubrir sus necesidades mínimas con 3 vitaminas V1, V2 y V3 al menor coste posible.
 |
|
Imagen modificada de cony.fu bajo licencia Creative Commons
|
La siguiente tabla muestra las dosis de cada vitamina que tienen 1 Kg de cada uno de los dos tipos de pienso:
| V1 |
V2 |
V3 |
|
| P1 |
4 | 2 |
1 |
| P2 |
1 | 1 | 2 |
Para que el alimento mezclado sea adecuado a las necesidades del perro debe contener, como mínimo, 8 dosis de V1, 6 de V2 y 6 de V3.
El coste de cada Kg de P1 es de 20 €, y el de cada Kg. de P2 de 10 €.
Vamos a ayudarles para saber en que cantidades tienen que mezclar los dos tipos de piensos para obtener un producto adecuado al menor coste posible. Sabemos que los dos tipos de pienso se venden por Kg, no pudiendo comprarse fraccionadamente, por lo que la solución debe ser de valores enteros.
1. Organicemos los datos
Vamos a llamar x a la cantidad de pienso P1 e y a la de pienso P2. Ponemos todos los datos en una tabla:
| Cantidad |
V1 | V2 |
V3 |
Coste |
|
| P1 | x | 4x | 2x | x | 20x |
| P2 | y |
y | y | 2y | 10y |
| Total | 4x+y |
2x+y | x+2y |
20x+10y |
Nuestro objetivo es minimizar los costes, por lo tanto, habrá que minimizar F(x,y)=20x+10y
Vamos con las restricciones. Las dos primeras son obvias: x≥0 e y≥0, es decir, la cantidad de cada una de los piensos debe ser positiva o nula.
Las otras tres restricciones saldrán de las cantidades mínimas de cada vitamina:
Vitamina 1 : 4x+y≥8 Vitamina 2: 2x+y≥6 Vitamina 3: x+2y≥6
Con lo que el planteamiento del problema será:
Min F(x,y)=20x+10y
Sujeto a
x≥0, y≥0
4x+y≥8
2x+y≥6
x+2y≥6
2. Representamos la región factible y resolvemos el problema
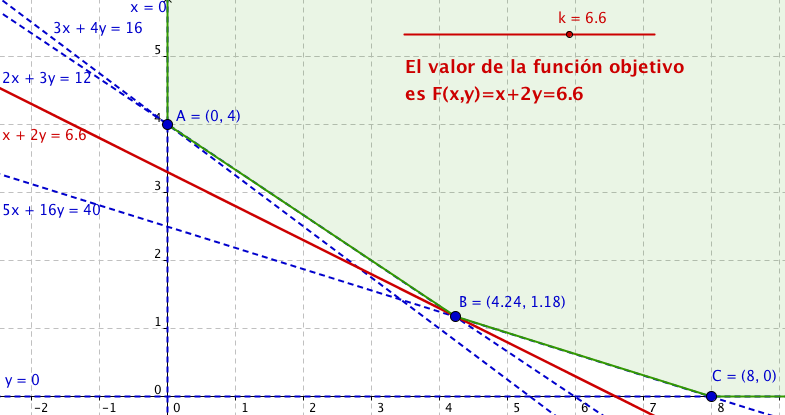
Como podemos ver en la siguiente escena de Geogebra la región factible es no acotada. Mueve el deslizador k para ver como se desplaza la función objetivo según el valor de ese número k.
3. Conclusión
Hay dos vértices B(1,4) y C(2,2) donde la función objetivo alcanza el mínimo. Como la solución tiene que ser entera, en ese segmento sólo están estos dos puntos con coordenadas enteras.
Si esto no fuera así serían solución todos los puntos del segmento BC. Observa que esto ocurre así porque la función objetivo es paralela a una de las restricciones.
Por lo tanto, en nuestro problema hay dos posibles soluciones:
- B(1,4) en esta primera posibilidad hay que mezclar 1 kg del Pienso 1 con 4 kg del Pienso 2. El coste es de 60 €.
- C(2,2) en este caso hay que mezclar 2 kg de Pienso 1 con 2 kg de Pienso 2. El coste es también de 60 €.
 |
| Imagen del Banco de Imágenes y sonidos del ITE |
La empresa de catering "Kerrico S. A." está diseñando un menú para un comedor escolar. El colegio les informa de que la dieta debe cumplir los siguientes requisitos:
- El número de calorías no ha de ser inferior a 2000.
- Debe contener un total de, al menos, 60 gr. de proteínas.
- Debe contener un total de, al menos, 80 gr. de grasas.
Para ello dispone de dos tipos de platos con las siguientes características:
| Calorías |
Proteínas |
Grasas |
|
| Primer Plato (100 gr.) |
250 |
10 |
15 |
| Segundo Plato (100 gr.) |
800 |
15 |
20 |
El precio de 100 gramos del primer plato es de 1 € y del segundo plato de 2 €.
Ayuda a esta empresa a calcular cuántos gramos se deben servir de cada plato para que el coste sea mínimo y cuál es ese coste.