2.1. ¡Que buena!

|
| Imagen modificada de yuichi.sakuraba bajo licencia CC |
La confitería "Tartasoro" es famosa por sus dos especialidades en tartas: la Tarta Imperial y la Tarta de Lima.
La Tarta de Imperial requiere para su elaboración medio kilo de azúcar y 8 huevos, y tiene un precio de venta de 16€. La tarta de Lima necesita 1 Kg de azúcar y 8 huevos, y tiene un precio de 20€. En el almacén quedan 10 Kilos de azúcar y 120 huevos.
Vamos a ayudarles para saber cuantas unidades de cada especialidad tienen que hacerse para obtener el mayor ingreso por ventas.
1. Organizamos los datos
Lo primero que haremos es organizar los datos en una tabla.
| Tartas |
Número |
Azúcar | Huevos |
Ganancias |
| Imperial |
x |
0,5x | 8x |
16x |
| Lima | y |
1y |
8y |
20y |
| Total | 0,5x+y | 8x+8y |
16x+20y |
Nuestro objetivo es maximizar las ganancias, por lo tanto, nuestro objetivo es maximizar la función F(x,y)=16x+20y
Las restricciones a nuestro problema son:
- Tanto x como y tienen que ser positivas o nulas, es decir: x≥0, y≥0.
- La cantidad de azúcar total no puede ser superior a 10 kg: 0,5x+y≤10.
- La cantidad de huevos tiene que ser inferior a 120 unidades: 8x+8y≤120.
Por lo tanto, el planteamiento de nuestro problema será:
Máx F(x,y)=16x+20y
Sujeto a
x≥0
y≥0
0,5x+y≤10
8x+8y≤120
2. Representamos la región factible
En este caso tenemos 4 desigualdades. Vamos a ayudarnos del programa Geogebra para hallar la región factible de nuestro problema.
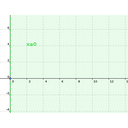
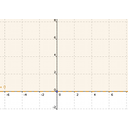
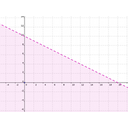
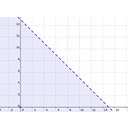
En la siguiente galería tienes las 4 imágenes correspondientes a la solución de cada una de las desigualdades.
3. Resolvemos el problema
En la siguiente escena de Geogebra podemos ver la región factible (Intersección de todas las restricciones). Moviendo el deslizador k, vemos como va variando la función objetivo y su valor.
4. Conclusión
En el punto Q(10,5) se obtiene el máximo valor de la función objetivo, que en este caso es 260.
Esto quiere decir que el máximo beneficio, 260 €, se obtiene cuando fabrican 10 Tartas Imperiales y 5 Tartas de Lima.
 |
| Imagen de Rubyran bajo licencia Creative Commons |
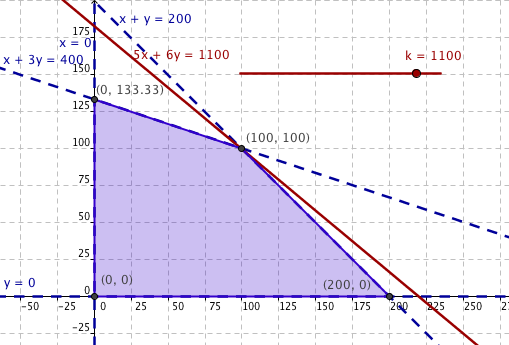
En la joyería "Mibrillante" fabrican pendientes y sortijas.
Para hacer unos pendientes se usan 2 gramos de oro y 1 gramo de plata , mientras que para hacer las sortijas necesitan 2 gramos de oro y 3 gramos de plata.
Los pendientes los venden a 50€ y las sortijas a 60€.
Disponen de 400 gramos de oro y 400 gramos de plata.
Ayuda a los joyeros a decidir cuántas joyas tienen que fabricar de cada tipo para obtener el máximo beneficio.