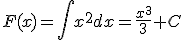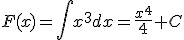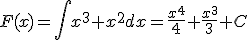1.1. ¿De dónde provengo?
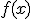 , su derivada es
, su derivada es 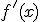 , pero si tenemos otra función
, pero si tenemos otra función 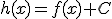 , siendo
, siendo 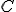 un número cualquiera, su derivada es
un número cualquiera, su derivada es 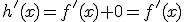 .
.
Así, la derivada de una función va a ser la misma si a esa función le sumamos un número cualquiera.
|
|
La pregunta que nos hacemos ahora es: si conocemos la función derivada de otra, ¿podemos conocer la función de la que es derivada?. En algunos casos es bastante sencillo de resolver. Por ejemplo, si tenemos la función 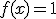 y sabemos que esta función es derivada de otra, la función de la que es derivada es
y sabemos que esta función es derivada de otra, la función de la que es derivada es 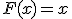 . Ya que sabemos que
. Ya que sabemos que
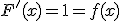
Pero teniendo en cuenta lo que hemos indicado más arriba, 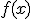 también es la función derivada de la función
también es la función derivada de la función 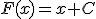 , siendo
, siendo 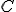 un número cualquiera.
un número cualquiera.
Si tenemos una función 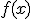 llamamos primitiva de
llamamos primitiva de 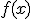 respecto a la variable
respecto a la variable 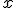 a la función
a la función 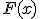 que cumple que:
que cumple que:
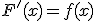
Tal como hemos visto, si 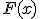 es una primitiva de la función
es una primitiva de la función 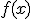 , también lo es
, también lo es 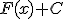 , siendo C un número cualquiera. Por eso llamamos integral indefinida de f(x) al conjunto de todas las primitivas de dicha función. Se representa de la siguiente forma:
, siendo C un número cualquiera. Por eso llamamos integral indefinida de f(x) al conjunto de todas las primitivas de dicha función. Se representa de la siguiente forma:
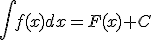
Al símbolo 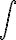 se le llama integral, a la función f(x) integrando y dx es la diferencial y nos indica respecto a qué variable se está hallando la integral.
se le llama integral, a la función f(x) integrando y dx es la diferencial y nos indica respecto a qué variable se está hallando la integral.
Tal como hemos visto anteriormente, si tenemos la función 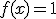 sabemos que:
sabemos que:
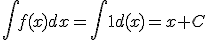
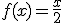 como la función derivada de una función
como la función derivada de una función 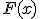 . Por tanto, para cada valor
. Por tanto, para cada valor  , la función
, la función 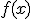 nos proporciona el valor
nos proporciona el valor 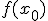 que es el valor de la pendiente de la recta tangente a la función
que es el valor de la pendiente de la recta tangente a la función 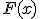 en el punto
en el punto 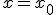 . En la parte de la derecha se van representado esas rectas tangentes. Observa que las mismas determinan la gráfica de una función. Esa función es
. En la parte de la derecha se van representado esas rectas tangentes. Observa que las mismas determinan la gráfica de una función. Esa función es 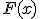 . Interactúa con la ventana cambiando el valor de
. Interactúa con la ventana cambiando el valor de  .
.
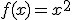
Calcula la integral de la función
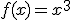
Calcula la integral de la función
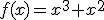
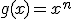 es
es 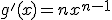
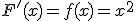 . Según lo que conocemos,
. Según lo que conocemos, 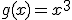 ya que
ya que 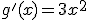 que es parecida a
que es parecida a 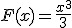 . En este caso tenemos que
. En este caso tenemos que 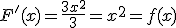 . ¡Ya lo tenemos!
. ¡Ya lo tenemos!
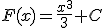 donde
donde