1.1. Dimensiones del lienzo
|
|
Vamos a comenzar el estudio completo de una función que desembocará en la representación gráfica de la misma. El primer punto de este estudio es el dominio. ¿Recuerdas cómo se calculaba el dominio de una función? Supongo que sí, aunque para hacer memoria observa el siguiente vídeo:
Vamos a dar el primer paso para representar gráficamente una función.
Consideramos la siguiente función racional: 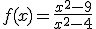
Perseguimos realizar la representación gráficamente esta función. Para ello, en esta ocasión te pedimos que calcules el dominio de la misma.
 |
La Empresa de Andrés y Ángela tiene un logotipo que puedes ver en la parte derecha. Como te indicamos en la historia inicial, una de los cometidos de la empresa es analizar el rozamiento de los vehículos con el aire cuando van circulando. Para ello utilizan el túnel del viento. A la empresa de Andrés y Ángela ha llegado el nuevo prototipo que ha diseñado una empresa de automóviles y quieren que analicen el rozamiento de este prototipo. Para hacerlo, en la empresa de Andrés y Ángela han metido el prototipo en el túnel del viento como puedes ver en el siguiente vídeo:
|
|
Tras meterlo en el túnel Ángela ha identificado cuatro funciones en el proceso que van a ser determinantes de cara a las conclusiones sobre el nuevo diseño. Estas funciones son:
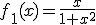 |
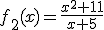 |
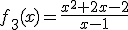 |
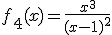 |
Ángela ha realizado el estudio completo de estas cuatro funciones para representarlas gráficamente. Andrés ha cogido todas las páginas del estudio de Ángela, ha tropezado y se le han caído todos los papeles desordenándolos. Ahora se propone ordenarlos y se ha dado cuenta de que, como Ángela es muy cuidadosa, en el estudio de cada una de las funciones ha utilizado un folio para cada apartado que necesita para representarla gráficamente. Te vamos a pedir que le ayudes a ordenarlos.
En esta ocasión, Andrés ha localizado los cuatro folios que corresponden al estudio del dominio de cada una de ellas. Ayúdale a identificar la función a la que corresponde cada uno de los folios. Para ello completa los espacios en blanco que aparecen seguidamente.
.- El folio que indica que el dominio de la función es 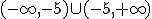 corresponde a la función
.
corresponde a la función
.
.- Existe un folio que no se ve bien ya que al caerse se ha mojado con agua. En este folio se indica que el dominio de la función f4 es 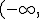 )
) (
(
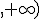 .
.
.- El folio que indica que el dominio de la función son todos los números menos el corresponde a la función .
.- El folio que indica que el dominio de la función son todos los números reales corresponde a la función .
|
|
Recuerda que otro de los aspectos que estudiamos de las funciones es la simetría. ¿Recuerdas cómo se hacía? De todas formas, en el siguiente ejemplo te lo aclaramos un poco:
Consideramos la siguiente función racional: 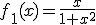
Perseguimos realizar la representación gráficamente esta función. Para ello, en esta ocasión te pedimos que estudies la simetría de la misma.
Andrés ha localizado ahora los cuatro folios correspondientes al estudio de la simetría de cada función. Recuerda que las funciones que Ángela había investigado eran:
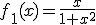 |
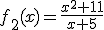 |
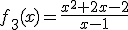 |
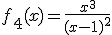 |
Ayúdale a identificar la función a la que corresponde cada uno de los folios. Para ello completa los espacios en blanco que aparecen seguidamente.
Escribe sí o no, según corresponda:
.- La función f1(x) es simétrica respecto al eje de ordenadas.
.- La función f1(x) es simétrica respecto al orígen de coordenadas.
.- La función f2(x) es simétrica respecto al eje de ordenadas.
.- La función f2(x) es simétrica respecto al orígen de coordenadas.
.- La función f3(x) es simétrica respecto al eje de ordenadas.
.- La función f3(x) es simétrica respecto al orígen de coordenadas.
.- La función f4(x) es simétrica respecto al eje de ordenadas.
.- La función f4(x) es simétrica respecto al orígen de coordenadas.
Consideramos la siguiente función racional: 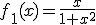
Perseguimos realizar la representación gráficamente esta función. Para ello, en esta ocasión te pedimos que calcules los puntos de corte con los ejes.
 |
Andrés ha localizado ahora los cuatro folios correspondientes al estudio sobre el punto de corte con los ejes de cada función. Recuerda que las funciones que Ángela había investigado eran:
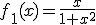 |
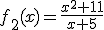 |
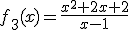 |
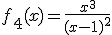 |
Ayuda a Ándrés a identificar la función a la que corresponde cada uno de los folios. Para ello completa los espacios en blanco que aparecen seguidamente.
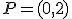 ,
, 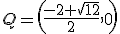 ,
, 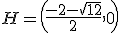 corresponde a la función
.
corresponde a la función
.
.- El folio que indica que el punto de corte con los ejes, de la función simétrica, es 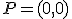 corresponde a la función
.
corresponde a la función
.
.- El folio que indica que la función, además de no tener simetrías, su punto de corte con los ejes es 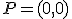 corresponde a la función
.
corresponde a la función
.
.- El folio que indica que el punto de corte con los ejes es 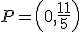 corresponde a la función
.
corresponde a la función
.
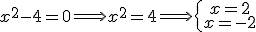
 es
es 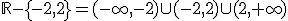 .
.
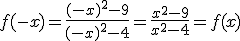
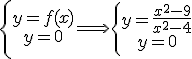
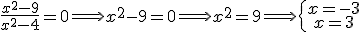
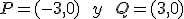 .
.
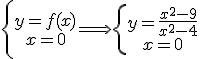
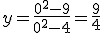 .
.
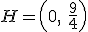 .
.