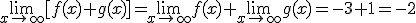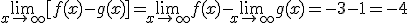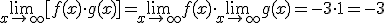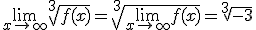1.1. Vamos a componer palabras.
¿Cual es el valor de una función cuando el valor de x tiende a un número a? La actuación más natural es sustituir el valor de a en la función y comprobar qué ocurre.
Veamos un ejemplo con la función f(x) = 2x + 1 y el 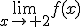
Si x se aproxima al valor +2, podemos construir la siguiente tabla.
| x | f(x) |
| 1,8 | 4,600 |
| 1,9 | 4,800 |
| 1,99 | 4,980 |
| 1,999 | 4,998 |
| 1,9999 | 4,9998 |
Pero también podemos sustituir el valor al que tiende la función en la función f(x), para tener una idea intuitiva del valor del límite. Si dicho valor pertenece al dominio y la función es continua, podemos concluir que f(a) es el límite.
Sean los siguientes límites 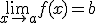 y
y 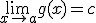 . Entonces:
. Entonces:
| Álgebra de límites | |
1. 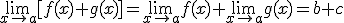 |
4. Si 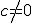 entonces entonces 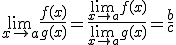 |
2. 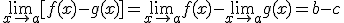 |
5. Si f(x) > 0 , 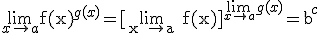 |
3. 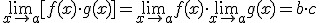 |
6. Si n es impar ó si n es par y 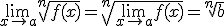 |
El valor a, puede ser un valor positivo, un valor negativo,
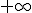 ó
ó 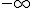
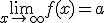 y
y 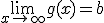 , entonces
, entonces 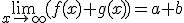 . Modifica a y b en el applets para obtener diferentes funciones.
. Modifica a y b en el applets para obtener diferentes funciones.
Sean 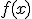 y
y 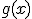 tal que
tal que 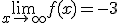 y
y 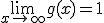 .
.
Calcula
1. 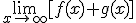
2. 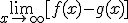
3. 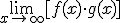
4. 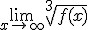
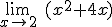 =
.
=
.
Determina el límite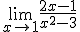
|
0
| |
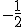
| |
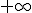
| |
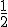
|
¿Qué ocurrirá con los límites cuando x tiende a 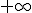 ? ¿El resultado siempre será
? ¿El resultado siempre será 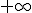 ?
?
¿Y cuando x tiende a 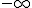 ?
?
Lo primero que debemos tener en cuenta es que al hacer el límite en el infinito de un polinomio, tan sólo debemos tener en cuenta el comportamiento en dicho infinito del término principal (el de mayor exponente). Dígamos que el monomio líder es cabeza de carrera y es el que determinará el lugar al que tenderá el límite.
Vamos a analizar el siguiente límite 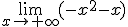 .
.
Para ello tan sólo habrá que estudiar el comportamiento en 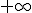 del líder, esto es:
del líder, esto es:
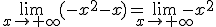
Obviamente, cuando x crece infinitamente, el valor de la función tiende no a 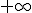 , sino a
, sino a 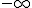 . Si analizas minuciosamente el por qué de la respuesta, te darás cuenta que esto es debido al coeficiente principal del polinomio
. Si analizas minuciosamente el por qué de la respuesta, te darás cuenta que esto es debido al coeficiente principal del polinomio 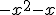 , igual a -1. El límite de una función polinómica cuando x tiende a
, igual a -1. El límite de una función polinómica cuando x tiende a 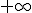 , depende del signo del coeficiente lider. Para calcular el límite, puedes comprobar que solo tenemos en cuenta el monomio de mayor grado.
, depende del signo del coeficiente lider. Para calcular el límite, puedes comprobar que solo tenemos en cuenta el monomio de mayor grado.
¿Y si x tiende a 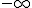 ? Analizamos el mismo límite
? Analizamos el mismo límite 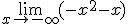 . Al elevar cualquier número negativo al cuadrado, obtendremos un número positivo, pero debido al coeficiente lider, obtendremos un límite igual a
. Al elevar cualquier número negativo al cuadrado, obtendremos un número positivo, pero debido al coeficiente lider, obtendremos un límite igual a 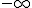 .
.
Si embargo si tratamos la función 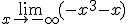 , obtendremos como límite
, obtendremos como límite 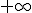 .
.
Has podido comprobar que la paridad del exponente solo interviene cuando el límite tiende a 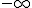
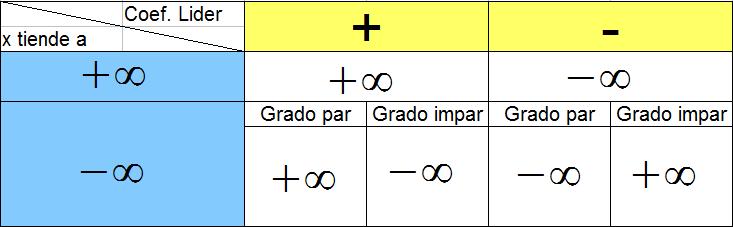
Debes tener en cuenta esta tabla a la hora de calcular los límites de raices de polinomios. Recuerda que no existe la raiz par de número negativos, por lo que no tiene sentido hablar del siguiente límite,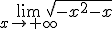 . Es recomendable para calcular límites de raices, determinar en primer lugar el límite del radicando.
. Es recomendable para calcular límites de raices, determinar en primer lugar el límite del radicando.
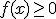 , entonces
, entonces