2. Perpendicular a dos bandas
 |
Seguro que cuando has estado paseando por algunas de las calles de tu ciudad has observado cables que cruzan de unos edificios a otros. Algunos pueden ser electricos, otros telefónicos. Incluso podemos recordar cables dedicados a un vídeo club privadoso cualquier otra temática.
Esas conexiones unen hilos de unas fachadas con otras Siempre están colocados de forma que la distancia que recorre por medio de la calle sea lo más corta posible, por lo tanto , suelen ser perpendiculares a las fachadas de las que salen.
En este apartado vamos a ver como calcular esas líneas que son perpendiculares a dos que ya tenemos.
El proceso es el siguiente :
- Hallamos un punto genérico P de la recta r (que dependerá de su parámetro, por ejemplo, t).
- Hallamos otro punto Q genérico de la recta r' (dependerá de otro parámetro s).
- Calculamos el vector
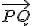 , que dependerá de dos parámetros.
, que dependerá de dos parámetros. - Imponemos que el vector anterior sea perpendicular a las dos rectas, r y r', y por lo tanto, los productos escalares por sus vectores de dirección deben dar cero.
- Nos queda un sistema de dos ecuaciones con dos incógnitas. Al resolverlo hallamos los valores de los parámetros t y s y por tanto los puntos P y Q que están sobre la perpendicular.
- Por último, la distancia entre las dos rectas que se cruzan es la distancia entre P y Q y la perpendicular común es la recta que pasa por P y Q.
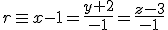 y
y 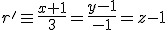 .
.
Si solo queremos hallar la recta que corta perpendicularmente a dos rectas que se cruzan, hay otro camino por el que podemos hacerlo. El proceso sería el siguiente.
- Hallamos un vector perpendicular a las dos rectas. Basta hallar el producto vectorial de los vectores dirección. Ese vector es el director de la recta buscada.
- Calculamos un plano que contenga a r y tenga el vector hallado antes como director.
- Determinamos otro plano que contenga a r' y al vector perpendicular hallado en el apartado 1.
- La recta buscada es la intersección de los dos planos hallados.
En el siguiente applet de Descartes puedes ver el proceso a medida que aumentas el pulsador Paso. Si pulsas con el botón derecho sobre la construcción aparece una ventana en la que puedes incluir los datos de las rectas que estás trabajando.
Applet de Descartes creado por Juan Simón Santamaría bajo licencia Creative Commons.
Un arquitecto ha diseñado un edificio de 20 plantas. Por el suelo del sótano del edificio pasa un tubo que recoge el agua sucia del edificio y por el suelo de la azotea pasa un tubo que recoge toda el agua de lluvia. Este agua de lluvia debe llevarse a la tubería del sótano. Para llevarla, el arquitecto debe hacerlo por el trazado más corto. Para conseguirlo ha calculado con su programa de diseño gráfico la ecuación de la recta de la tubería de la azotea, resultando ser:
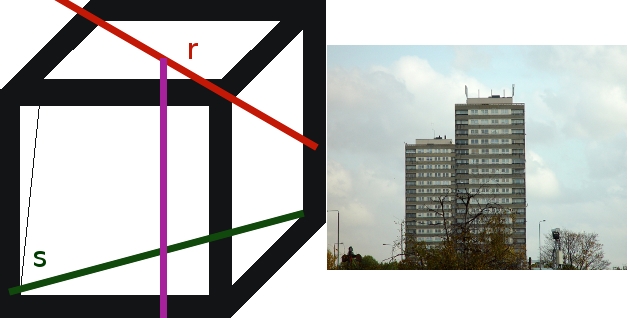 |
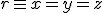
Tambien ha calculado la ecuación de la recta que sigue la tubería del sótano, resultando ser:
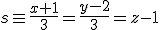
Sabe que ambas rectas se cruzan en el edificio, por lo que únicamente debe calcular la perpendicular común a las dos rectas. Intenta ayudarle.
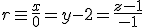 y
y 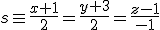 . Calcula también la distancia entre las dos rectas.
. Calcula también la distancia entre las dos rectas.
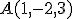 y tiene de vector dirección
y tiene de vector dirección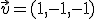 . La recta r' para por
. La recta r' para por 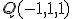 y tiene como dirección
y tiene como dirección 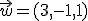 . A simple vista vemos que los dos vectores de dirección no son proporcionales, luego las dos rectas tienen distinta dirección. Para comprobar que se cruzan consideramos el vector
. A simple vista vemos que los dos vectores de dirección no son proporcionales, luego las dos rectas tienen distinta dirección. Para comprobar que se cruzan consideramos el vector 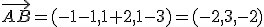 y vemos si es linealmente independiente de los dos anteriores. Para ello basta hallar el determinante formado por los tres.
y vemos si es linealmente independiente de los dos anteriores. Para ello basta hallar el determinante formado por los tres.
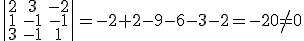
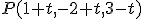 de r y un punto
de r y un punto 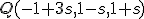 de r'.
de r'.
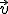 y
y 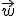 el vector:
el vector: 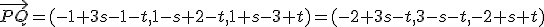 .
.
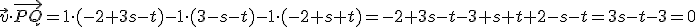
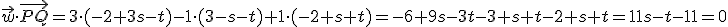
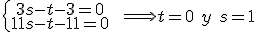 .
.
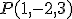 y
y 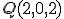 .
.
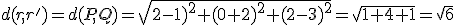 .
.
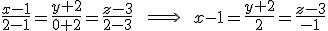
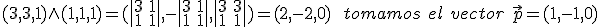
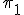 que contiene a la recta r y al vector
que contiene a la recta r y al vector 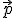 .
.
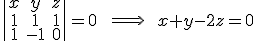
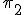 que contiene a la recta s y es perpendicular a las dos rectas y, por tanto, contiene a
que contiene a la recta s y es perpendicular a las dos rectas y, por tanto, contiene a 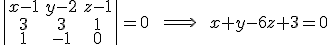
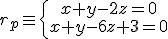
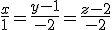 . Ten presente que tu puedes haber considerado otro punto y un vcetor director que sea proporcional al anterior. Basta que compruebas si el punto que has utilizado pertenece a esa recta y si los vectores son proporcionales.
. Ten presente que tu puedes haber considerado otro punto y un vcetor director que sea proporcional al anterior. Basta que compruebas si el punto que has utilizado pertenece a esa recta y si los vectores son proporcionales.