1.4. ¡Será por planos!
 |
En la vida cotidiana es usual que nos encontremos con la confluencia de más de dos elementos. Es fácil encontrarse con tres o más planos en los lugares más corrientes. Por ejemplo, en la esquina de cualquier habitación suelen coincidir tres planos, el techo o suelo, y dos paredes contiguas. En cualquier estantería nos encontramos con varios planos paralelos. También es corriente encontrar dos planos paralelos cortados por una transversal, por ejemplo, de nuevo en casa, el techo y el suelo suelen ser dos planos paralelos y cualquier pared corta a ambos planos. Y así en multitud de casos.
En este último apartado vamos a estudiar la posición relativa de tres planos, lo que es muy fácil de estudiar pues si consideramos el sistema formado por las ecuaciones de los tres planos,
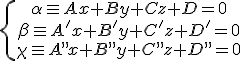
vemos que lo que hay que estudiar es un sistema de tres ecuaciones con tres incógnitas, exactamente lo mismo que hicimos en el tema 4 de la unidad anterior. Lo único que tendremos que hacer es estudiar todos los casos que pueden darse en ese sistema.
 |
| rango(Mc)=rango(Ma)=3 |
Consideramos la matriz ampliada del sistema anterior: 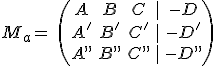 en la que vamos a estudiar todos los casos posibles.
en la que vamos a estudiar todos los casos posibles.
1) Si rango(Mc)=3 entonces obligatoriamente rango(Ma)=3, el sistema es compatible determinado y hay una única solución. Los tres planos tienen un punto común.
2) Si rango(Mc)=2 y rango (Ma)=3 el sistema es incompatible y no hay ningún punto común a los tres planos. En este caso podemos tener varios casos.
 |
| rango(Mc)=2 y rango(Ma)=3 Tres planos formando un prisma. |
2-1) Si las tres filas de la matriz de los coeficientes son independientes dos a dos, cada dos planos se cortan en una recta independiente del otro plano. Los planos forman un prisma. Un ejemplo sería el prisma triangular típico de la caja de chocolates Toblerone o si pensamos en las paredes y el suelo de una tienda de campaña canadiense.
2-2) Si una de las filas de la matriz de los coeficientes es proporcional a otra, entonces tenemos dos planos paralelos cortados por otro plano.
3) Si rango(Mc)=rango(Ma)=2 el sistema es compatible indeterminado. Hay infinitos puntos soluciones. Como depende de un parámetro (pues el número de incógnitas es 3 y el rango 2, las soluciones dependen de 3-1 = 1 parámetro) la solución es una recta. Es decir, en este caso los tres planos se cortan en
 |
| rango(Mc)=2 y rango(Ma)=3 Dos planos paralelos y el otro secante. |
una recta. Pero podemos tener también dos casos:
3-1) Si las tres filas de la matriz de los coeficientes sin independientes dos a dos, los tres planos tienen distinta dirección y pasan por una misma recta. Formarían parte de un haz de planos tal como vimos en el apartado 1.2.
3-2) Si una de las filas es proporcional a otra, en este caso tenemos dos planos coincidentes y el tercer plano lo corta en una recta.
4) Si rango(Mc)=1 y rango(Ma)=2 el sistema es incompatible, es decir, no hay punto común a los tres planos. Vuelve a haber dos casos.
 |
| rango(Mc)=1 y rango(Ma)=2. Tres planos paralelos |
4-1) Si no hay ninguna fila de la matriz ampliada que sea proporcional a otra, los tres planos son paralelos entre sí.
4-2) Si dos filas de la matriz ampliada son proporcionales, entonces dos de los planos son coincidentes y el tercero es paralelo a los otros dos.
5) Si rango(Mc)=rango(Ma)=1 entonces los tres planos son coincidentes.
En la siguiente dirección tienes una página donde aparece la misma clasificación pero en la que se incluye n dibujos esquematizados de las distintas posiciones relativas y algún ejercicio resuelto.
Indica la posición de los siguientes grupos de planos.
a) 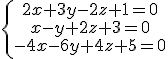 b)
b) 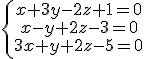 c)
c) 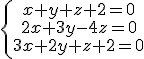
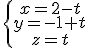 .
.