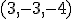1.3. Uno de cada
Ya hemos visto las posiciones relativas de dos elementos del espacio cuando son iguales. ¿Qué pasará si elegimos uno de cada tipo? Pues que las posiciones relativas serán las mismas que en el caso del plano. Imagina un lanzador de jabalina. Si hace bien el tiro, al terminar la jabalina quedará clavada sobre el suelo, si se equivoca la jabalina quedará sobre el plano del suelo y cuando la ha lanzado, habrá momentos en que la jabalina esté paralela al suelo.
Antes de ver los casos los vamos a comprobar gráficamente. En la siguiente escena de Descartes puedes escribir la ecuación de un plano de coeficientes Ax+By+Cz+D=0 (el plano verde que aparace en la imagen) y una recta indicando las coordenadas del punto P y las del vector dirección 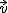 . Para incluir los coeficientes puedes utilizar los controles o escribir los valores en las casillas y pulsar Intro. Si pulsas sobre la ventana y mueves un poco el ratón, el sistema de ejes comenzarán a girar, con lo que podrás verlo desde distintos lugares. Se para volviendo a hacer clic.
. Para incluir los coeficientes puedes utilizar los controles o escribir los valores en las casillas y pulsar Intro. Si pulsas sobre la ventana y mueves un poco el ratón, el sistema de ejes comenzarán a girar, con lo que podrás verlo desde distintos lugares. Se para volviendo a hacer clic.
Dibuja los siguientes pares de elementos y observa las distintas posiciones.
a) 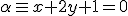 y
y 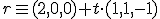
b) 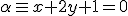 y
y 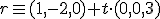
c) 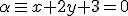 y
y 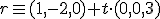
 |
| Ilustración de Gustavo Doré, imagen de dominio público de Wikimedia Commons. |
Las posiciones relativas de una recta y un plano en el espacio son las siguientes.
a) La recta y el plano se cortan en un punto. Cuando la dirección de la recta es linealmente independientes de las dos direcciones del plano.
b) La recta es paralela al plano. Cuando la dirección de la recta es linealmente dependiente de las dos direcciones del plano y no hay ningún punto de la recta en el plano.
c) La recta está contenida en el plano. Cuando la dirección de la recta es linealmente dependiente de las dos direcciones del plano y cualquier punto de la recta está en el plano.
Para estudiar algebraicamente la posición relativa de una recta y un plano tomamos la ecuación general del plano y la paramétrica de la recta: 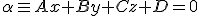 y
y 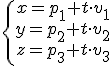
Basta sustituir las expresión de la recta en el plano y obtenemos una ecuación con una incógnita t.
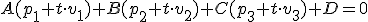 operamos en la expresión y obtenemos
operamos en la expresión y obtenemos
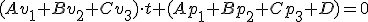 los dos paréntesis son números, llamémoslos f y g.
los dos paréntesis son números, llamémoslos f y g.
Estudiamos la ecuación resultante f·t+g=0.
- Si f es distinto de cero, se puede despejar la t y existe una única solución. La recta corta al plano en un punto.
- Si f es cero, pero g no, obtendríamos la ecuación 0·t+g=0 con g no nulo. Esta ecuación es imposible, por lo que no hay solución. La recta es paralela al plano.
- Si f y g son ambos cero, nos queda la ecuación 0·t+0=0 que se verifica para todo valor de t, luego todos los puntos de la recta están en el plano y, por tanto, la recta está incluida en el plano.
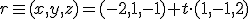 y del plano
y del plano 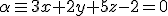 .
.
Halla las posiciones relativas de los siguientes pares de elementos.
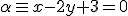 y
y 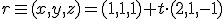
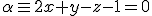 y
y 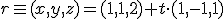
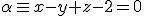 y
y 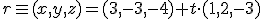
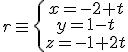 y la sustituimos en el plano.
y la sustituimos en el plano.
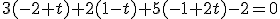 y ahora desarrollamos y simplificamos
y ahora desarrollamos y simplificamos
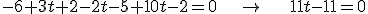 cuya solución es t=1.
cuya solución es t=1.
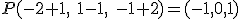 .
.