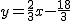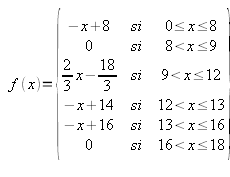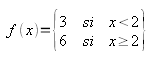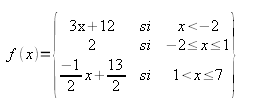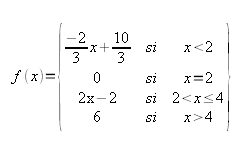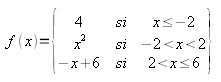1.2. Y ahora, al revés
Fíjate en esta curiosa gráfica que muestra el tiempo de espera de una persona que acude a un centro de salud según la hora de la mañana a la que va.
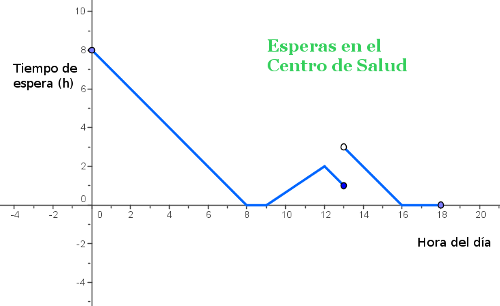 |
Puedes ver que en este Centro, la consulta empieza a las 8 de la mañana, así que si se te ocurre ir a las 12 de la noche (0 horas) vas a tener que esperar hasta las ocho de la mañana.
Además, a las 2 de la tarde paran las consultas dos horas, para que el personal sanitario y administrativo pueda ir a comer, por lo que a las 13 h (1 de la tarde) dejan de recibirse pacientes para el turno de mañana, teniendo que esperar entonces al turno de tarde, donde la consulta está abierta de 4 a 6 de la tarde (desde las 16 hasta las 18 h.)
Si te fijas, mirando la gráfica podemos saber cuánto tiempo debe esperar una persona que va a las 6 de la mañana, o a las 8:45, o a las 17h, pero no se ve tan claro el tiempo que debe esperar si acude a las 10:15 o a las 12:30.
Con objeto de mejorar el servicio, los responsables del centro han acudido a la asesoría de Eva y Evaristo para que les ayuden a mejorar estos tiempos de espera. Éstos, lo primero que van a hacer es poner el tiempo de espera como una función. ¿Se podrá encontrar la expresión analítica de la función que da el tiempo de espera según la hora a la que llega el paciente?
Vamos a ver que sí, que es posible, y puesto que nuestra gráfica está formada por trozos de rectas, la función será una función a trozos.
Vamos a ver si lo has entendido.
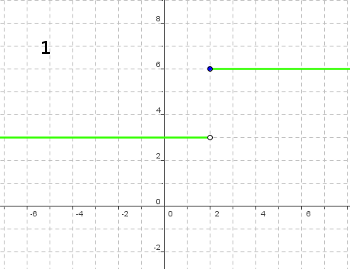
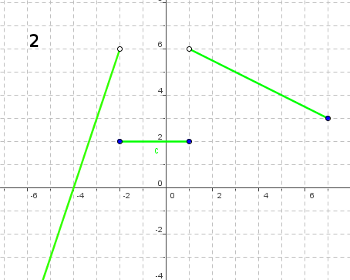
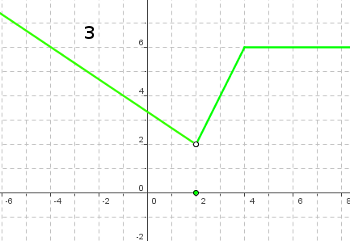
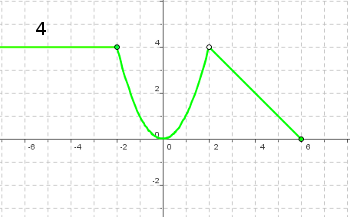
Cógete papel y lápiz y averigua la fórmula que le corresponde a cada una de las cuatro gráficas siguientes:
 |
 |
 |
 |