2.2. La recta que fijan la curva.
Pero no sólo las funciones del tipo y = k/x se representan por una gráfica de ese estilo. Hay otras muchas.
Y a modo de ejemplo vamos a ver la siguiente.
Ejemplo o ejercicio resuelto
 |
| 4 Imagen de emezeta.com bajo licencia Creative Commons. |
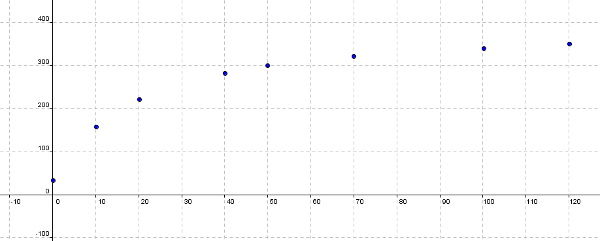
En la oficina donde trabaja Patricia, han organizado un curso para que los empleados adquieran más destreza a la hora de teclear en el ordenador. El responsable del curso, Carlos Morris, afirma que con su método, a medida que se va aumentando la práctica, se van aumentando las pulsaciones por minutos, y es más, afirma que tiene una función que da el número de pulsaciones según las horas de clases que haya dado, y ésta es :
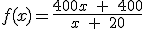
Ahora bien, uno de los socios de la notaría, que está contratando los servicios del Señor Carlos Morris, le plantea la cuestión de cuántas clases son necesarias, a lo que Carlos le contesta: - mientras más, mejor-.
Patricia, que está un poco puesta, le dice a su jefe que va a llegar un momento en el que la evolución apenas se va ir notando y que entonces ya no merecería la pena seguir. ¿Irá creciendo y creciendo la cantidad de pulsaciones o habrá un tope hasta el que por muchas clases prácticas que demos, ya no podremos superar esa cantidad de pulsaciones por minuto?
Vamos a ver cómo se comporta esta función.
Pero, ¿cómo sería la gráfica si nos salimos del contexto del problema, es decir, dándole valores negativos?
Pues algo así:
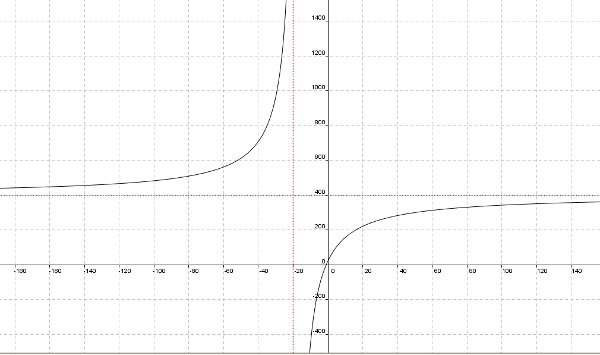
Como puedes ver, la forma es muy similar a la de proporcionalidad inversa cuando "k" es negativo, sólo que se ha desplazado un poco para la izquierda y para arriba, es decir, en lugar de pegarse ahora a las rectas que forman los ejes coordenados, se pegan a las rectas, y = 400 y x = - 20.
Actividad
Como puedes ver en la siguiente escena, todas las funciones de la forma:
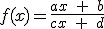
se representan gráficamente mediante una hipérbola.
En la escena puedes modificar los coeficientes a, b, c y d y poner la función que desees, así como modificar el punto P y ver las coordenadas de cualquier punto sobre la función.
Applet Descartes modificado del original de Marta García Neira bajo licencia Creative Commons.
Actividad
Las rectas a las que se pega una función se llaman asíntotas de la función.
Las funciones que estamos viendo se llaman funciones racionales y tienen dos asíntotas; una vertical y otra horizontal.
Objetivos
El concepto de asíntota, matemáticamente se presenta cuando al acercarnos a un punto la función tiende a infinito, o al hacer que "x" se vaya a infinito, la función tiende a un número.
La tendencia de una función, como veremos en la próxima unidad, se expresa por un límite y, para ir abriendo boca, la cosa iría así:
La recta x =a es una asíntota vertical de una función f(x) si:
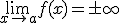
Esto quiere decir que cuando en el eje X nos acercamos al valor "a", la función se va a infinito.
La recta y = L es una asíntota horizontal de una función f(x) si:
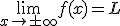
lo que quiere decir, que tenemos una asíntota horizontal si al alejarnos en el eje OX, la función, cada vez más,se va acercando a una altura concreta, L.
En el siguiente enlace puedes profundizar un poco más sobre el cálculo y el significado de asíntota.