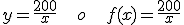2.1. Función de proporcionalidad inversa.
Ejemplo o ejercicio resuelto
 |
En el próximo puente vamos a hacer un viaje a la capital de la Gran Bretaña, a Londres. Como vamos un grupo bastante numeroso, hemos decidido alquilar un autobús para que nos lleve hasta el aeropuerto de Málaga que es donde cogemos el vuelo. El dueño de la empresa de transporte nos pide 200 € por hacer el viaje.
¿Cómo escribimos esto como una relación?
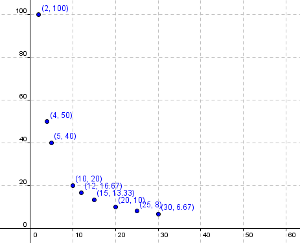
Pero, ¿qué pasaría con esta función si nos salimos del contexto del problema y a x le damos valores positivos muy pequeños, o valores muy grandes o valores negativos?
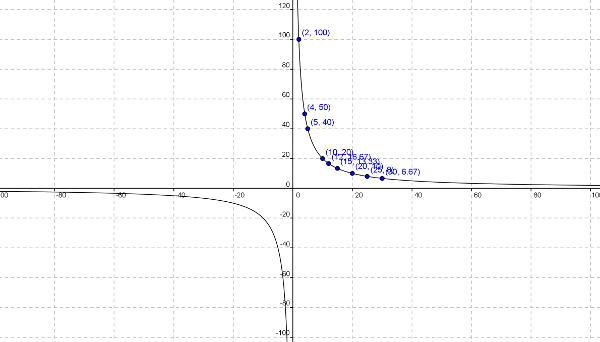
Pues la respuesta es que la gráfica que nos saldría sería de la forma:
Actividad
Las funciones de la forma:
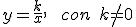
se llaman funciones de proporcionalidad inversa, y como puedes ver en la siguiente escena, modificando el valor de "k", todas tienen una gráfica similar, formando una curva llamada hipérbola y pegándose a los ejes de coordenadas.
Applet Descartes de José Luis Alonso Borrego bajo licencia Creative Commons.
Pre-conocimiento
Actividad
La función de proporcionalidad inversa tiende a pegarse a dos rectas, una vertical y otra horizontal. Si recuerdas de tema anterior, éstas son:
- Vertical: la recta x = 0
- Horizontal: la recta y = 0.
AV - Pregunta de Elección MúltipleRelaciona cada gráfica con su expresión algebraica. Si tienes dudas en alguna de las expresiones, lo mejor es que le des un valor a "x", obtengas la "y" y compruebes si ese punto pertenece o no a la gráfica dibujada.
1) 
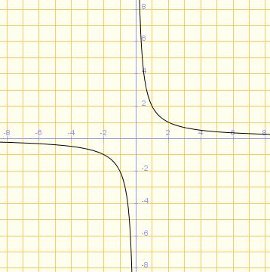La gráfica corresponde a la función:
|
y = 1/x
| |
|
y = -1/x
| |
|
y = 2/x
| |
|
y = -2/x
|
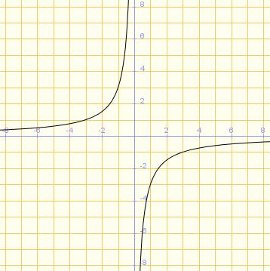La gráfica corresponde a la función:
|
y = -3/x
| |
|
y = 3/x
| |
|
y = 3x
| |
|
y = -3x
|