1.1. Estos son mis atributos
En los temas del bloque de Análisis, hemos estado estudiando conceptos acerca de las funciones que hemos ido poniendo en práctica conforme se iban desarrollando.
En este tema, a modo de colofón, los usaremos todos juntos, con el objetivo de realizar e interpretar la representación gráfica de las funciones. Definición de función, dominio, cortes con los ejes, continuidad, límites para el cálculo de asíntotas, ... y haremos uso especialmente de las derivadas para el estudio de la monotonía (cálculo de máximos y mínimos relativos) y de la curvatura (obtención de puntos de inflexión)
En muchos ámbitos de nuestra vida, es conveniente guiarnos por un determinado procedimiento a la hora de realizar un trabajo. Es por ello, por lo que hemos considerado conveniente, seguir el mismo esquema para todos los estudios de representaciones gráficas que llevemos a cabo en la unidad.
Dicho esquema, se detalla a continuación, a modo de cuadro resumen:
|
CUADRO RESUMEN PARA PARA REPRESENTAR FUNCIONES Función: f(x) = ____________
|
||||||||||||||||||
|
||||||||||||||||||
Vamos a recordar de manera breve algunas definiciones de conceptos ya estudiados y procedimientos ya vistos en temas anteriores, para que puedas afrontar con garantías el resto del tema.
Concretamente, trataremos: monotonía (crecimiento y decrecimiento), máximos y mínimos, curvatura (concavidad y convexidad), puntos de inflexión y asíntotas.
Cuando hablamos de monotonía, nos estamos refiriendo al comportamiento de una función respecto a su crecimiento o decrecimiento. Una función f derivable es:
· Creciente en el intervalo (a,b) si· Decreciente en el intervalo (a,b) si
Una función f continua y derivable en un intervalo (a,b), alcanza sus máximos y mínimos relativos en los puntos del intervalo (a,b) en los que f '(x)=0. Además, si estudiamos la segunda derivada:
· Máximo relativo: f '(x)=0 y f ''(x)<0· Mínimo relativo: f '(x)=0 y f ''(x)>0
En una función dos veces derivable, podemos estudiar la curvatura de la siguiente forma:
· Convexa (U): será convexa en los intervalos donde f ''(x) > 0También puedes acceder a un ejemplo de estudio paso a paso de la curvatura de una función. Basta pulsar en el siguiente enlace.
Por último, para terminar el repaso, te dejamos la siguiente presentación sobre asíntotas, recordando su definición, tipos y algunos ejemplos.
Vamos a poner en práctica nuestros conocimientos interpretando la siguiente gráfica:
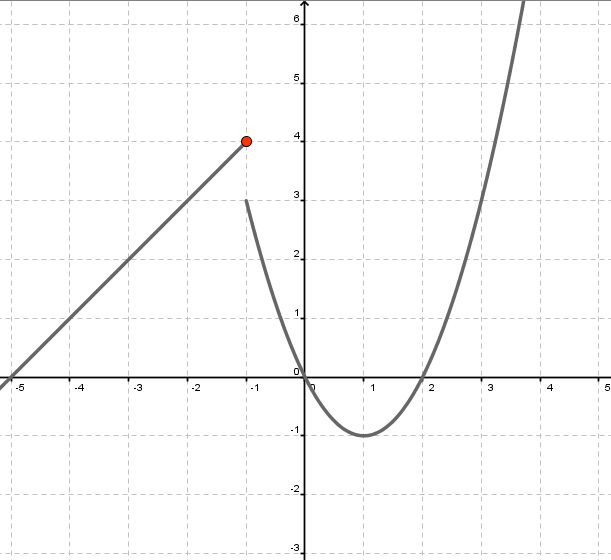
Las siguientes cuestiones siguen el orden expuesto en el cuadro resumen anterior, a fin de que vayas recordando los principales atributos de las funciones.
1. ¿A qué tipo de función corresponde la gráfica?
2. ¿Cual es el dominio de la función?
3. ¿Es discontinua en algún punto? ¿Qué tipo de discontinuidad presenta?
4. ¿Presenta algún tipo de simetría?
5. ¿Y asintotas tiene?
6. ¿La derivada primera se anula en su máximo relativo? ¿Por qué?
7. ¿Cual es el mínimo relativo de la función?
8. ¿Qué podemos afirmar sobre su monotonía?
9. ¿Cual es su recorrido?
En el portal En Silicio se dedican principalmente a:
Explorar la realidad usando datos y gráficas
¿Quieres conocer algunos de sus estudios? Visítala.
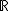
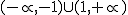 y decreciente en (-1,1)
y decreciente en (-1,1)