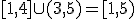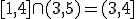3.1. Intervalos (desde... hasta...)
Puede que alguna vez, al ir a comprar unas entradas, te hayas encontrado con una lista de precios como ésta:
| Infantil (de 0 a 12 años) |
5 € |
| Joven (de 12 a 18 años) |
9 € |
| Adulto (mayores de 18 años) |
15 € |
En nuestra vida diaria establecemos muchos límites: de edad, de velocidad, por precios, alturas, horarios... Y en ocasiones no está del todo claro si el límite que establecemos forma parte de una categoría u otra (por ejemplo, un chico de 12 años que comprara una entrada del caso anterior ¿sería entrada infantil o joven?)
En Matemáticas tenemos una herramienta muy útil para hacer referencia a los conjuntos que queremos establecer. Mira los siguientes ejemplos:
| Horario de apertura: |
Límite de velocidad: |

|

|
| Mentira de fluzo, CC by 2.0 |
minimum speed limit de TheTruthAbout, CC by-sa 2.0 |
| El intervalo [10 ; 22] indica que estamos considerando cualquier hora entre las 10h y las 22h, incluyendo ambas. | Con el intervalo [40 ; 75] decimos que estamos obligados a conducir a una velocidad que esté entre 40 y 75 km/h. No nos vale ningún valor por debajo de 40 ni por encima de 75. |
| Altura mínima: |
Altura máxima: |

|

|
| This High de LarimdaME, CC by-nc 2.0 | Imagen de Iván Santiesteban, CC by 2.0 |
| Para subir en esta atracción debes medir como mínimo 1,20m. Podríamos expresarlo como el intervalo [1,20 ; +∞), aunque es evidente que no tiene mucho sentido incluir alturas superiores a 2,60 o 2,70m. |
En este aparcamiento podría entrar cualquier vehículo que tenga entre 0 y 2,30m de altura. Sería el intervalo [0 ; 2,30]. |
Ya que tienes una idea básica, en el siguiente enlace (que pertenece a la EDAD) vas a aprender qué son los intervalos y qué tipos hay. De las pestañas superiores, sólo tienes que fijarte en la de "Contenidos", que es la que se presenta a continuación. Pulsa el icono de la flecha naranja para avanzar:
|
[2 ; 5] | |
|
(2 ; 5) | |
|
[2 ; 5)
|
|
(-2 ; +∞)
| |
|
(-2 ; +∞]
| |
|
(-∞ ; -2)
|
|
3,423
| |
|
3,31
| |
|
3,2
|
Con los intervalos podemos hacer algunas operaciones:
a) Unión ( ): al unir dos intervalos, consideramos los números que están en uno u otro intervalo:
): al unir dos intervalos, consideramos los números que están en uno u otro intervalo:
b) Intersección ( ): la intersección de dos intervalos consiste en quedarse con los números que están en los dos a la vez:
): la intersección de dos intervalos consiste en quedarse con los números que están en los dos a la vez: