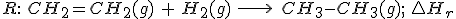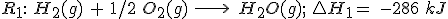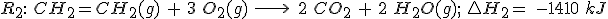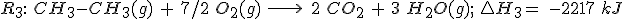2.1 Aplicando la ley de Hess
 |
| Imagen 11 Dr T, Creative commons |
En 1840, Hess demostró experimentalmente que la cantidad de calor puesta en juego en un reacción a presión o volumen constante no depende del camino seguido y es independiente de que el proceso transcurra en una o más etapas (ley de Hess).
A esta misma conclusión ya hemos llegado anteriormente mediante la termodinámica (ΔU = Qv ; ΔH = Qp), ya que si ambos calores son funciones de estado, no dependen del camino seguido en la transformación. Por lo tanto, la ley de Hess no debería considerarse como una ley independiente, pero sucede que la Termoquímica es históricamente anterior a la Termodinámica, y cuando ésta estableció sus principios, aquélla ya había enunciado sus leyes y tenía sus propios convenios.
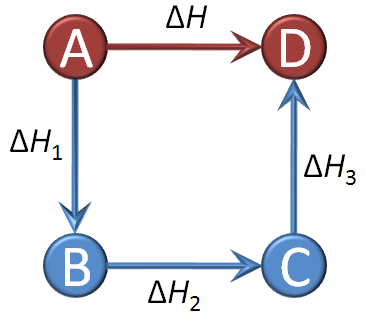
Fíjate en la imagen. La reacción de la que queremos saber su ΔH es A → D. Pero esa reacción se puede producir de forma directa (A produce D) o en tres fases:
Reacción 1: A → B; ΔH1
Reacción 2: B → C; ΔH2
Reacción 3: C → D; ΔH3
La reacción directa es la resultante de estas tres: A se transforma en B, pero B lo hace en C y C en D, con lo que, globalmente, A se transforma en D. Este razonamiento se puede expresar matemáticamente diciendo que la reacción global es la suma de las tres reacciones: si escribes como reactivos totales todos los reactivos de las tres reacciones y haces lo mismo con los productos, obtienes
A + B + C → B + C +D
que, eliminando B y C que aparecen tanto en reactivos como en productos, se transforma en A → D.
En general, la reacción global no se obtiene como suma de las reacciones, sino que hay que multiplicarlas por un número (si intervienen dos moles de una sustancia, pero en una reacción solamente aparece uno, habrá que multiplicar esa reacción por dos) o incluso darle la vuelta, transformando los reactivos en productos y los productos en reactivos (multiplicando por -1).
 |
| Imagen 12 Elaboración propia |
Ley de Hess
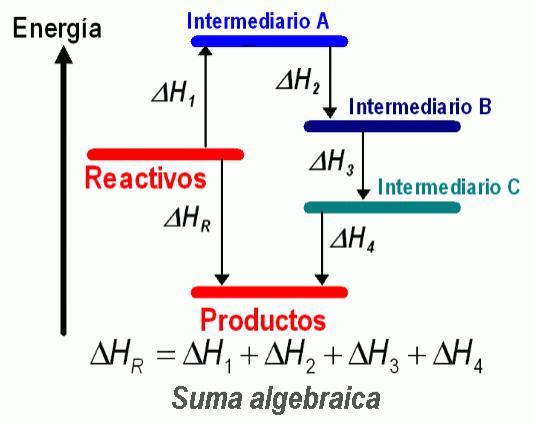
Desde el punto de vista práctico, se puede decir que si una reacción se puede escribir como combinación lineal de otras, su variación de entalpía es la misma combinación lineal de las variaciones de entalpía de las reacciones combinadas.
En el caso de la imagen, como R = R1 + R2 + R3 + R4 entonces ΔHR= ΔH1 + ΔH2 + ΔH3 + ΔH4.
 |
| Imagen 13 Vindaloo, Dominio público |
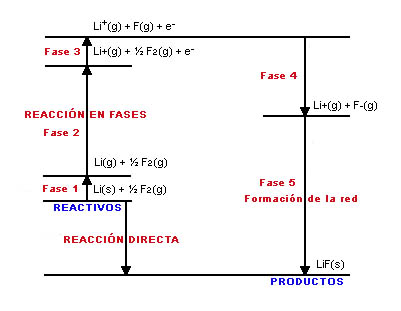
Observa la imagen, en la que se representan las distintas reacciones que intervienen en la formación de un cristal iónico de LiF (el ciclo de Born-Haber).
Fíjate en que la reacción puede producirse de forma directa o en fases: sublimar el litio, disociar el flúor, ionizar ambos átomos y permitir que interaccione una gran cantidad de los iones formados para dar lugar a la sustancia iónica (la energía desprendida en este último paso se llama energía de red).
Suponiendo que conoces las variaciones de entalpía de todos los procesos, excepto la energía de red, aplica la ley de Hess para determinar la energía de red a partir del resto de datos.