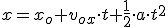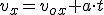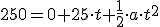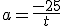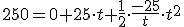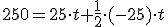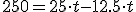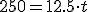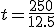1.3 Plano horizontal con rozamiento

Imagen de elaboración propia

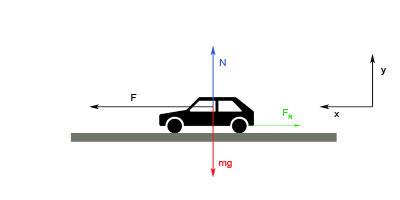
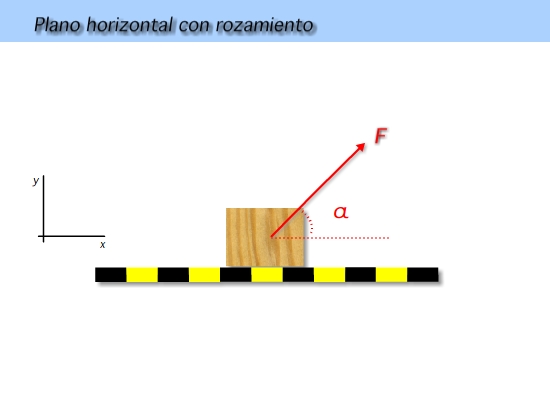
Ahora vas a estudiar un caso un poco más complicado del problema anterior. Vamos a estudiar el movimiento de un cuerpo sometido a una fuerza que se desliza sobre un plano horizontal con rozamiento. En principio supondremos que la fuerza aplicada es suficiente para modificar el estado de movimiento del objeto que originalmente está en reposo. De este modo podemos aplicar la fórmula para calcular la fuerza de rozamiento FR que se opondrá al posible deslizamiento de ambas superficies.

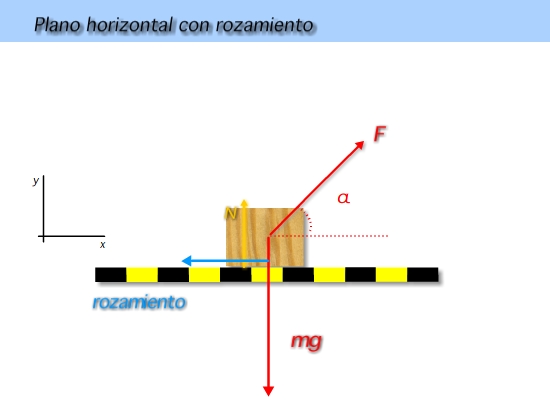
Hacemos un esquema y dibujamos todas las fuerzas que actúan sobre nuestro cuerpo.

Imagen de elaboración propia

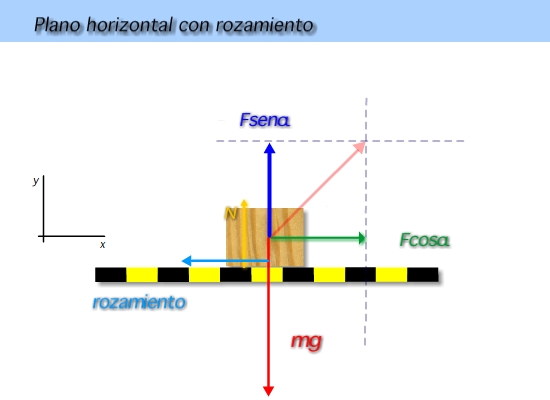
Elegimos un sistema de referencia adecuado y descomponemos las fuerzas que no sean parelela a ninguno de ambos ejes en sus componentes cartesianas.

Imagen de elaboración propia

 

 

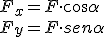
Ahora aplicamos la 2ª ley de Newton a ambos ejes. En el vertical supondremos que no hay aceleración:

 

 

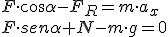
Teniendo en cuenta que el valor de la fuerza de rozamiento en este caso, en que suponemos que el cuerpo está deslizando, es FR = μ·N, puede escribirse:

 

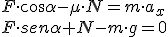
Obtenemos un sistema de dos ecuaciones con dos incógnitas que puedes resolver fácilmente.

Icono IDevice Actividad
En los problemas con rozamiento debes recordar siempre que existen dos tipos de coeficiente de rozamiento (μ), y utilizar uno u otro en función del caso que tengas que resolver:
  • Si el cuerpo no ha comenzado a moverse la fuerza de rozamiento tiene un valor desconocido y será una de las incógnitas del problema.
  • Si el cuerpo está a punto de moverse o quieres calcular en qué momento comienza a hacerlo utilizarás el coeficiente de rozamiento estático (μe).
  • Si el cuerpo ya se encuentra en movimiento, utilizarás el coeficiente de rozamiento dinámico (μd).

Icono de iDevice Ejemplo o ejercicio resuelto
Miniatura coche
Un automóvil de 1000 kg de masa recibe la propulsión de su motor como una fuerza en dirección horizontal. Sabiendo que los coeficientes de rozamiento estático y dinámico de sus neumáticos con el asfalto en seco son μe= 0.8 y μd= 0.6 respectivamente, se pide que respondas a las siguientes cuestiones:
a) Dibuja el diagrama de fuerzas y escribe las ecuaciones correspondientes a la situación planteada.

b) ¿Qué fuerza mínima deberá suministrar el motor para que el automóvil comience a moverse?

c) ¿Cuál será la fuerza necesaria para mantener el movimiento con velocidad constante?

d) ¿Cuál será la aceleración que imprimirá al automóvil una fuerza de 10000 N?

e) De repente, el conductor observa un obstáculo en la calzada a una distancia de 250 m. Si la velocidad en ese momento es de 90 km/h y el conductor coloca la marcha en punto muerto, ¿qué fuerza de frenado mínima (F) deberá ejercerse para que el vehículo no colisione con el obstáculo?

Icono de iDevice AV - Reflexión
Cuando el asfalto está mojado, el coeficiente de rozamiento disminuye drásticamente hasta valores tan bajos como μe = 0.3 y μd = 0.25 respectivamente. ¿Cómo variarán las fuerzas necesarias respecto a las calculadas en el apartado anterior? ¿Será esto positivo a la hora de la conducción del automóvil?

Imagen de Dash bajo licencia Creative Commons BY SA


« Anterior | Siguiente »