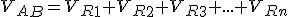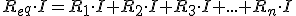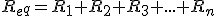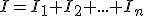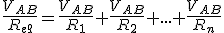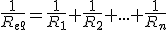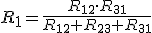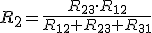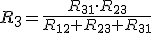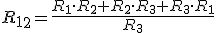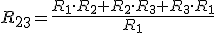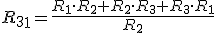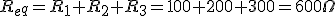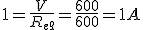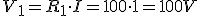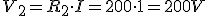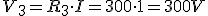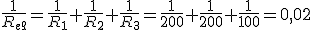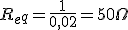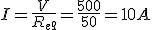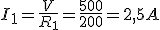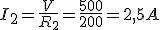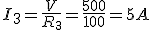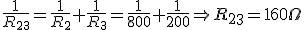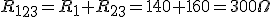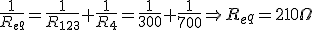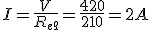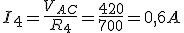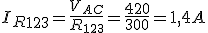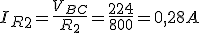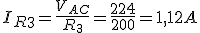7. Asociación de resistencias

Todos los receptores o en nuestro caso las Resistencias, se pueden asociar y nos simplifica mucho a la hora de hacer ciertos cálculos como veremos más adelante. Recordaremos las formas básicas de asociación: Serie y paralelo, y después veremos 2 formas nuevas de asociación de resistencias: Estrella y Triangulo, asociaciones muy utilizadas en los motores trifásicos... Os toca sacar la calculadora... ¡A trabajar!

Animación 2. Asociación de resistencias. Fuente: Banco de Imágenes del ITE

Licencia: Creative Commons

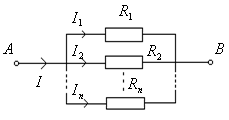
En un circuito eléctrico, es frecuente encontrarnos con más de una resistencia y en estos casos, a fin de proceder al estudio de dicho circuito, es conveniente poder simplificarlo, procediendo a asociar estas resistencias. Para ello se sustituyen dos o más resistencias por una única llamada resistencia equivalente, que consume la misma energía que el conjunto de las sustituidas. Esta asociación puede ser:

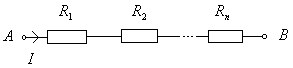
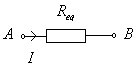
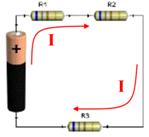
ASOCIACIÓN EN SERIE.

ASOCIACIÓN EN PARALELO.

ASOCIACIÓN MIXTA.

ASOCIACIÓN EN ESTRELLA Y EN TRIÁNGULO

ASOCIACIÓN EN SERIE:

Sus características:

Se conecta una resistencia a continuación de otra.

La intensidad de corriente que circula por ellas es la misma.

La diferencia de potencial a la que está sometida cada una depende del valor óhmico de la resistencia.

La suma de las diferencias de potencial de cada resistencia, será igual a la diferencia de potencial a la que se encuentre sometida la resistencia equivalente.

Imagen 30. Imagen de elaboración propia.

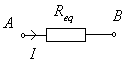
Teniendo en cuenta la Ley de Ohm:

Dividiendo por I, obtenermos:

Luego podemos decir que la resistencia equivalente de una asociación de dos o más resistencia en serie tiene un valor óhmico igual al resultado de sumar el valor de las resistencias que queremos asociar.

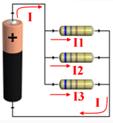
ASOCIACIÓN EN PARALELO:
Sus características:

Se conectan las resistencias, de tal forma que tengan sus extremos conectados a puntos comunes.

La intensidad de corriente que circula por la resistencia equivalente es igual a la suma de las intensidades que circulan por cada una de las resistencias que estamos asociando.

La diferencia de potencial a la que están sometida cada resistencia es la misma que la existente en sus extremos común.

Imagen 31. Imagen de elaboración propia.

Como podemos observar:

Teniendo en cuenta la Ley de Ohm:

De donde fácilmente se puede deducir que:

Así, podemos decir que la inversa de la resistencia equivalente a una asociación en paralelo de dos o más resistencias, es igual a la suma de las inversas de las resistencias que estando en paralelo queremos asociar a fin de calcular su resistencia equivalente.

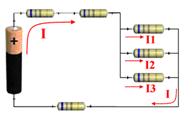
ASOCIACIÓN MIXTA DE RESISTENCIAS:

Se entiende por asociación mixta, cuando existe una combinación de resistencias en serie y en paralelo.
Para el cálculo de la resistencia equivalente de esta combinación de resistencias, se procede a resolver por separado las agrupaciones serie (primero) y paralelo, anteriormente estudiadas.
Si el circuito es complejo, muchas veces es conveniente, ir dibujando los diferentes circuitos resultantes de los pasos intermedios dados en cada agrupación, facilitando así los cálculos posteriores. Todo esto, se verá más claramente en la resolución del los diferentes ejercicios que se plantean.

Imagen 32.Imagen de elaboración propia.

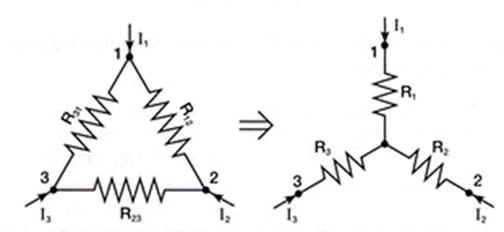
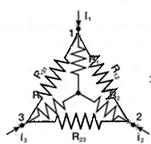
ASOCIACIÓN EN ESTRELLA Y EN TRIÁNGULO:

Este tipo de asociaciones, que tienen su importancia en diversos circuitos electrotécnico, como en el arranque de motores eléctricos (que se verá en unidades posteriores a esta), se explicarán directamente sobre su formulación matemática a través de su esquema, sin entrar en su demostración.

Configuración estrella

Configuración triángulo

Imagen 33. Imagen de elaboración propia.

Para transformar una conexión triángulo en estrella:

Para transformar una conexión estrella en triángulo:

Si imaginamos la siguiente figura, y observándola detenidamente, en que están superpuestas ambas configuraciones, se podrán aprender mejor las anteriores fórmulas.

Posteriormente, cuando en siguientes temas, se traten los términos admitancia e impedancia, sería conveniente revisar estas fórmulas. Para profundizar en lo dicho ver:

http://es.wikipedia.org/wiki/Teorema_de_Kenelly

Para completar el aprendizaje de esta pregunta, es necesario realizar múltiples ejercicios, a fin de adquirir destreza en su realización así como manejar adecuadamente las unidades oportunas (siempre que sea posible en el S.I.).

Imagen 34. Imagen de elaboración propia

Ejemplo o ejercicio resuelto

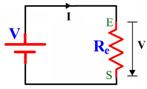
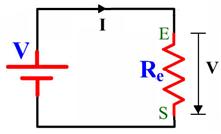
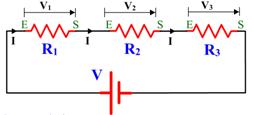
Dado el circuito de la figura, sabiendo que R1=100Ω, R2=200Ω, R3=300Ω y V=600V, calcular:

La resistencia equivalente a las tres dadas.
El valor de la intensidad que circula por el circuito.
El valor de las tensiones en cada resistencia

Imagen 35. Imagen de elaboración propia.

Ejemplo o ejercicio resuelto

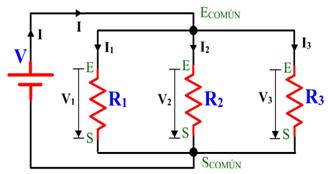
Dado el circuito de la figura, donde R1=200Ω, R2=200Ω, R3=100Ω y V=500V, calcular: La resistencia equivalente a las tres dadas. El valor todas las intensidades que circula por el circuito.
	Imagen 37. Imagen de elaboración propia.

Ejemplo o ejercicio resuelto

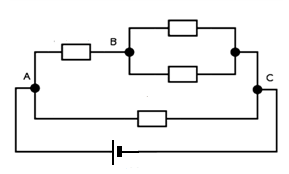
Dado el circuito de la figura, donde R1=140Ω, R2=800 Ω, R3=200 Ω, R4=700 Ω y V=420V, calcular:

Resistencia equivalente.
Calcular todas las intensidades y tensiones existentes en el circuito.

Imágen 39.

Licencia: Creative Commons.

Procedamos a su resolución, pero en esta ocasión, no se irán dibujando los circuitos parciales resultantes (con la representación de cada intensidad y cada caída de tensión), dejando esta necesaria labor al alumno, a fin de que contribuya a la resolución del ejercicio.

1. Calculamos la resistencia equivalente a R₂ y R₃, que al estar en paralelo, tendremos:

Observamos que esta resistencia calculada R₂₃ queda en serie con R₁ por lo que podemos establecer una nueva asociación de resistencias que dará como resultado:

Por últimos tenemos R₁₂₃ en paralelo con R₄ que resolviendo como sabemos:

2. Veamos ahora el cálculo de las intensidades y tensiones, tomando como referencia el nombre de los nudos señalados en el circuito (recuerdo que el alumno debe ir dibujando todo esto).

La intensidad total es decir la que sale de la pila (y por el convenio visto entra en el nudo A):

Como la tensión V_AC=V=420, podemos decir que:

Con la misma consideración anterior, la intensidad que pasa por R₁₂₃ será:

Observamos de nuevo que la suma de estas dos últimas intensidades es igual a la intensidad total calculada anteriormente.

Solo nos resta calcular las intensidades que recorren las resistencias R₂ y R₃ ya que evidentemente por R₁ pasarán los 1,3A calculados anteriormente (R₁ está en serie con R₂₃ por lo que son recorridas por la misma intensidad). Procedamos:

Previamente realicemos algunos cálculos de tensiones como V_AB y V_BC:

V_AB = R₁·I_R₁₂₃ = 140·1,4 = 196V

Y como sabemos que V_AC = V_AB + V_BC podemos decir que:

V_BC = V_AC - V_AB = 420 - 196 = 224V

Continuando con el pretendido cálculo de las intensidades restantes:

Hemos de observar que también se cumple que, la suma de estas dos últimas intensidades calculadas es igual a la intensidad que entraba en el nudo B (1,4 A).

« Anterior | Siguiente »

	1. Observamos que las tres resistencias están en serie, luego para calcular la resistencia equivalente, solo tendremos que sumar:
Imagen 36. Imagen de elaboración propia.
También podemos observar en el circuito de la figura, que la tensión a la que estaría sometida esa resistencia equivalente, seria 600 V.
2. Para calcular el valor de la intensidad, recurrimos a la Ley de Ohm:

3. Por último se nos pide el valor de V1, de V2 y de V3, que podemos calcular de nuevo, haciendo uso de la Ley de Ohm:

Es importante darse cuenta de que la suma de las tensiones V1, V2 y V3 da como resultado la tensión total V (600V).

1. En este caso se trata de resistencia asociadas en paralelo, con lo cual para calcular su resistencia equivalente, tendremos que recurrir a:
	Luego:
Imágen 38. Licencia: Creative Commons.
2. En este segundo apartado, hemos de observar previamente, que tenemos cuatro intensidades: I₁, I₂, I₃ e I. La primera "I" es la intensidad total del circuito, que podemos calcular aplicando la Ley de Ohm en la R_eq, esto es: Para el cálculo de las otras tres intensidades I1, I2 e I3, hemos de mirar el circuito original (no el equivalente) y vemos que las tres resistencias están sometidas a la misma tensión V, luego aplicando la Ley de Ohm a cada elemento, obtenemos: Este ejercicio queda resuelto, pero para su pleno aprovechamiento, hemos de realizar dos consideraciones: Si sumamos las intensidades I1, I2 e I3, observamos que coincide con el valor de I (lo que nos puede servir para verificar si el problema ha sido bien realizado). Por las resistencias de más alto valor óhmico, va menos intensidad (los electrones circulan "más alegremente" por donde menos resistencia encuentran).