3.1. Transformaciones
En este apartado vamos a estudiar cómo transformar una circunferencia en una elipse y un romboide en un cuadrado y en un rectángulo.
Entre los elementos de las figuras afines siempre existirá una característica común:
- En el caso de la circunferencia y la elipse ambas deben compartir al menos un diámetros y un eje.
- En el caso del romboide y el cuadrado, o el rectángulo, ambos son paralelogramos.
Curvas cónicas, Determinación de los puntos de una Elipse mediante afinidad.
En este caso los diámetros de la circunferencia coinciden con los ejes dados de la elipse.
Transformación afín de un cuadrilátero en cuadrado.
Tenemos que determinar la dirección de afinidad, para ello tenemos que considerar el ángulo que forman las diagonales del cuadrado.
Transformación afín de un cuadrilátero en paralelogramo rectángulo.
En este caso para determinar la dirección de afinidad es necesario conocer el ángulo que forman una diagonal con un lado del paralelogramo rectángulo, también se puede resolver si conocemos el ángulo que forman las diagonales entre sí.
También se puede realizar la transformación afín de una circunferencia en elipse a partir de los diámetros conjugados, en este caso determinamos una serie de puntos de la curva cónica, pero no los ejes, por lo que el trazado es más complejo; para simplificarlo podemos aplicar el procedimiento estudiado en el apartado 3.1 del tema 1 de esta unidad didáctica.
En la animación inferior puedes ver cómo se determinan mediante afinidad los puntos de una elipse dados sus diámetro conjugados.
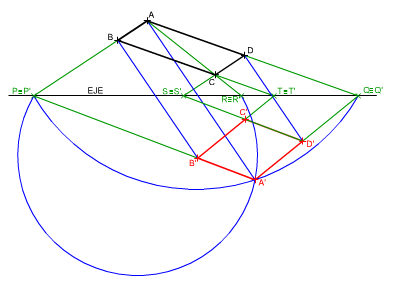 |
En la imagen de la izquierda te mostramos cómo se ha transformado un cuadrilátero ABCD en un paralelogramo rectángulo A'B'C'D'. Te pedimos que realices dicha transformación. Material necesario:
|