2.1. Triángulos y Cuadriláteros

Icono IDevice Actividad
Para seguir avanzado en el conocimiento de la afinidad en algunos ejercicios las figuras originales están cortadas por el eje de afinidad, por tanto, es necesario que repases los conceptos y procedimientos basados en los puntos dobles.

Transformación afín de un triángulo.

En la siguiente animación te mostramos cómo trazar un triángulo afín A'B'C' al dado ABC según una afinidad determinada por un punto doble y dos lados afines, el eje de afinidad corta a la figura original.


 

Transformación afín de un cuadrilátero.

En este caso el cuadrilátero es un paralelogramo rectángulo lo que facilita mucho la resolución de este ejercicio, ya que los lados afines serán también paralelos entre sí.
En la animación inferior puedes ver cómo se transforma el paralelogramo ABCD según una afinidad determinada por un par de puntos afines y el eje de afinidad.

 

Icono de iDevice Caso de estudio
 

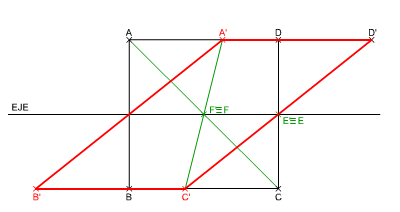En la imagen de la izquierda puedes ver cómo se ha trazado un cuadrilátero afín a un cuadrado dado ABCD, según una afinidad determinada por dicho paralelogramo, el eje y un punto afín D', te pedimos que:
Dibujes el cuadrilátero afín A'B'C'D'.

Material necesario:

  • Lápiz blando y duro.
  • Compás.
  • Plantilla de dibujo (escuadra y cartabón).
  • Hojas para realizar trazados de prueba.
Para realizar este ejercicio debes descargar este documento pdf.  

« Anterior | Siguiente »