3.2. Alfabeto
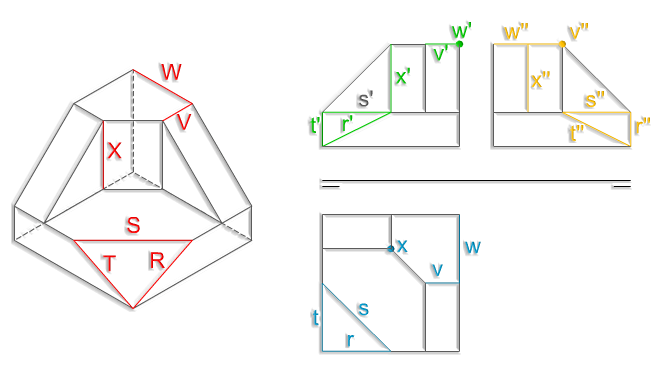
En este apartado vamos a estudiar las distintas posiciones que ocupa la recta respecto de los planos de proyección, los planos bisectores y el plano de perfil, analizando las características que presentan sus proyecciones.
RECTAS CONTENIDAS EN LOS PLANOS DE PROYECCIÓN:
- Contenida en el PVP: todos su puntos tienen alejamiento cero, luego su proyección horizontal está confundida con la línea de tierra.
- Contenida en el PHP: todos sus puntos tienen cota cero, luego su proyección vertical está confundida con la línea de tierra.
- Contenida en la LT: todos sus puntos tienen cota y alejamiento cero, luego sus proyecciones, vertical y horizontal, están confundidas con la línea de tierra.
RECTAS PARALELAS A UNO O DOS PLANOS DE PROYECCIÓN:
- Recta horizontal: paralela al PHP y oblicua al PVP. Pasa por dos cuadrantes.
- Recta frontal: paralela al PVP y oblicua al PHP. Pasa por dos cuadrantes.
- Recta paralela a la LT: paralela al PVP y al PHP. Sólo pasa por un cuadrante.
- Recta de punta: perpendicular al PVP y paralela al PHP. Pasa por dos cuadrantes.
- Recta vertical: perpendicular al PHP y paralela al PVP. Pasa por dos cuadrantes.
RECTAS OBLICUAS A LOS PLANOS DE PROYECCIÓN:
- Recta oblicua: todos sus puntos tienen distinto origen cota y alejamiento, por tanto, sus proyecciones son oblicuas respecto de la LT. Pasa por tres cuadrantes.
- Recta perfil: todos sus puntos tienen el mismo origen; pero su cota y alejamiento son distintos, sus proyecciones son perpendiculares a la LT. Pasa por tres cuadrantes.
- Recta que pasa por la LT: tiene un punto situado en la LT. Pasa por dos cuadrantes.
En el caso de las rectas de perfil encontramos que pueden ser de dos tipos:
- Primer tipo: rectas en las que todos sus puntos cumplen la siguiente propiedad: a mayor cota menor alejamiento.
- Segundo tipo: rectas en las que todos sus puntos cumplen la siguiente propiedad: a menor cota menor alejamiento.
Lo puedes ver en la siguiente animación:
RECTAS PARALELAS A LOS PLANOS BISECTORES:
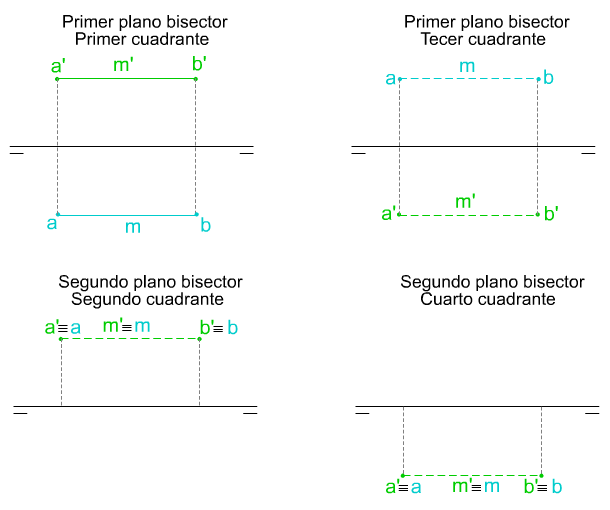
- Paralela al primer plano bisector: todos sus puntos tienen distinto origen, cota y alejamiento (salvo uno). Sus proyecciones (vertical y horizontal) son oblicuas respecto de la LT y forman el mismo ángulo con ella.
- Paralela al segundo plano bisector: todos sus puntos tienen distinto origen, cota y alejamiento (salvo uno). Sus proyecciones (vertical y horizontal) son oblicuas respecto de la LT y paralelas entre sí; forman el mismo ángulo con la LT.
RECTAS PARALELAS A LA LT CONTENIDAS EN LOS PLANOS BISECTORES.
Todos los puntos de estas rectas tienen la misma cota y alejamiento, por estar contenidos en un plano bisector, y como además son paralelas a la LT, sus proyecciones estarán representadas a igual distancia de la LT.
Aunque solamente hemos analizado el alfabeto de la recta en el primer cuadrante, en este tipo de rectas tenemos que hacer una excepción:
- Contenidas en el primer plano bisector: las proyecciones están representadas a igual distancia respecto de la LT a ambos lados de la misma.
- Contenidas en el segundo plano bisector: las proyecciones están representadas a igual distancia respecto de la LT, pero confundidas.
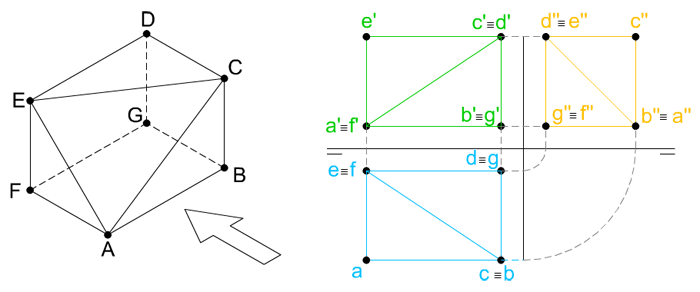
Dadas las vistas diédricas (alzado, planta y perfil izquierdo) de la pieza ABCDEFG, determina qué tipo de rectas son sus aristas.