DEFINICIÓN:

Es el principio de la medida y de la extrema razón. Se encuentra en los seres vivos: animales, plantas, insectos, etc., por eso se le suele llamar el número de la Naturaleza; racional por su presencia y su lógica e irracional por su valor numérico
Los griegos fueron los primeros en utilizar la sección áurea debido a sus estudios matemáticos y a su deseo de hallar una relación, un orden, como símbolo de vida y armonía. Este número fue designado con la letra griega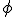

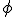(= 1,618...), también se llamó número áureo (Leonardo da Vinci) y es la medida media y la razón última que define la sección áurea.
Vitruvio (arquitecto romano del siglo I a. de C.): "Para que un todo, dividido en partes desiguales, resulte hermoso, es necesario que exista una relación entre la mayor y la menor parte, igual que la existente entre la mayor y el todo". a/b = c/a.

SEGMENTO ÁUREO:

Es la división de un segmento en media y extrema razón, es decir, la división de una longitud tal que la parte menor es a la más grande como la más grande es a la longitud total.
El método para determinar la sección áurea es el que sigue:

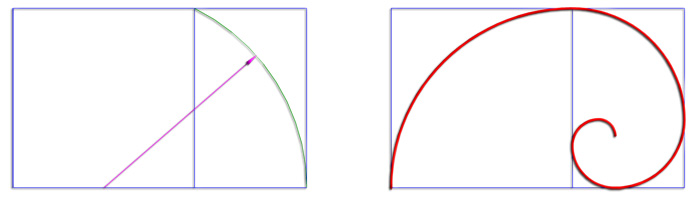
RECTÁNGULO ÁUREO:

Es aquél cuya proporción es tal que el lado mayor, divido por el menor da como resultado el número áureo ().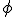
El método para determinar el rectángulo áureo es:

APLICACIÓN: construcción de un pentágono regular conocida la diagonal.

El lado de un pentágono regular es el segmento áureo de su diagonal.