1.2 Tercera y cuarta proporcional
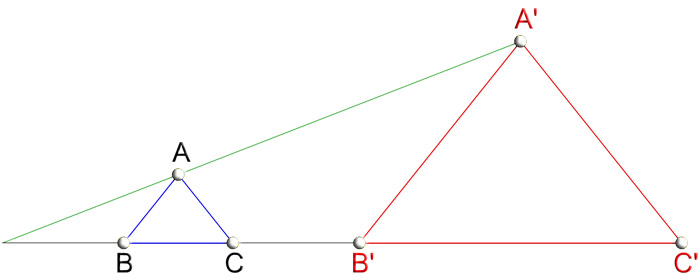
En geometría la proporción se da entre segmentos y para que estos queden perfectamente definidos usamos sus vértice, por tanto, esta transformación se dibuja usando la siguiente nomenclatura: los vértices los puntos proporcionales se representan en mayúscula (las letras), sin prima para los originales (A, B, C, 1, 2...). y con prima para los transformados (A', B', C', 1', 2'...).
DIVISIÓN DE UN SEGMENTO EN PARTES PROPORCIONALES: primero vamos a recordar cómo se dividía un segmento en partes iguales.
PROPORCIONALIDAD DE SEGMENTOS:
La razón entre dos segmentos es el valor de la relación entre las magnitudes de ambos segmentos, siendo a, b, c y d los términos de la proporción.
Cuando relacionamos dos razones establecemos una proporción (proporción es la igualdad de dos razones: a/b= c/d).
La razón entre dos segmentos es el valor de la relación entre las magnitudes de ambos segmentos, siendo a, b, c y d los términos de la proporción.
Cuando relacionamos dos razones establecemos una proporción (proporción es la igualdad de dos razones: a/b= c/d).
- A los términos a y d se les denomina extremos.
- A los términos b y c se les denominan medios.
- A los términos a y b se les denominan antecedentes.
- A los términos c y d se les denominan consecuentes.
TERCERA PROPORCIONAL:
Cuando dos de los términos conocidos (extremos o medios) tienen el mismo valor cualquiera de los otros recibirá el nombre de tercera proporcional. a/b = b/x.
CUARTA PROPORCIONAL:
Cuando se conocen tres de los cuatro términos, se puede obtener el cuarto, éste recibe el nombre de cuarta proporcional. a/b = c/x.
APLICACIONES:
- Multiplicación de segmentos:
- División entre segmentos: